前ページ|次ページ
第8章では、仮説検定に入る前段階として、確率分布、正規分布や標本調査について解説していきます！
少し高校で習う範囲を超えてしまう為、統計学を勉強した事がない人にとっては、知らない単語が多く、本連載講座の中で最も難しい章になってしまうかもしれません。
しかし、統計分野のほとんどの基礎となる部分なので、何回も読んで理解しながら進んでいってほしいです！
また、本講座では、統計学を用いてデータ分析が出来るようになってもらう事が目標である為、データ分析をする上で理解しておけばいい事に絞って説明しています。
その為、統計学自体について詳しく知りたい方は、0から学ぶ確率・統計講座の以下の様な、記事を参考にして下さい！
https://www.tech-teacher.jp/blog/statistics_6_distribution/
また、本章で用いるExcelファイルは以下からダウンロードして下さい！
本連載講座【Excelによる統計解析講座】では、Excel未経験の方、自身の無い方でも順を追って学習でき、基礎からデータ分析に必要なスキルまでを身に付ける事が出来ます。
画像が多く、ビジュアルで理解しやすくなっておりますので、読み物が得意ではないという方も大丈夫です！
また、第７章からは、統計学の分野も扱う為、様々な方に役立つ講座となっております。
そのため、
- Excelを仕事で使う可能性のある方
- Excelに自信のない方
- データ分析をExcelでやりたい方
等は是非、TechTeacherが運営する【Excelによる統計解析講座】を使って学習していって下さい！
〈目次〉
第1章：【テーブル】Excelのテーブル（フィルター）を解説！
第2章：【SUM,AVERAGE】Excelの基本的な関数を解説！
第3章：【XLOOKUP,COUNTIF】データ分析の為のExcel関数を解説！
第4章：【棒,折れ線,散布図】Excelの基本的なグラフを解説！
第5章：【ピボットテーブル】Excelの便利機能”ピボットテーブル”を紹介！
第6章：【プレゼン資料】Excelグラフの体裁の整え方について解説！
第7章：【相関分析】相関係数と共分散をExcelを用いて解説！
第8章：【確率変数・正規分布】確率変数や正規分布をExcelで解説！
第9章：【t検定・z検定】母平均と母分散の仮説検定について解説！
第10章：【t検定・z検定】2つの集団の母平均・母比率の仮説検定を解説！
第11章：【仮説検定】カイ二乗検定とF検定をExcelで一瞬で解く！
統計学の基礎に触れよう
では、早速、確率分布とは何かから学んでいきましょう！
確率変数と確率分布とは
ある事象（現象）が起こる度合いを0から1までで表したものを確率と言います。
ここで、試行の結果にXという数を割り当てた時、このXを“確率変数”と言います。
これだけでは分からないと思うので、さいころを2つ振った時の和の確率を考えてみましょう。
例えば、3という数字は、[1,2]、[2,1]と出た時の2パターンで、さいころの目が同様に確からしい（全て等しい確率で出る）とすると、
\[ \text{和が3になる確率}=\frac{2}{6\times6}=\frac{1}{18} \]
より、2つのさいころを振った時、その目の和が3になる確率は\(\frac{1}{18}\)となります。
これを、1から12の全てについて求めていくと、その確率は以下の様にグラフに表せます。
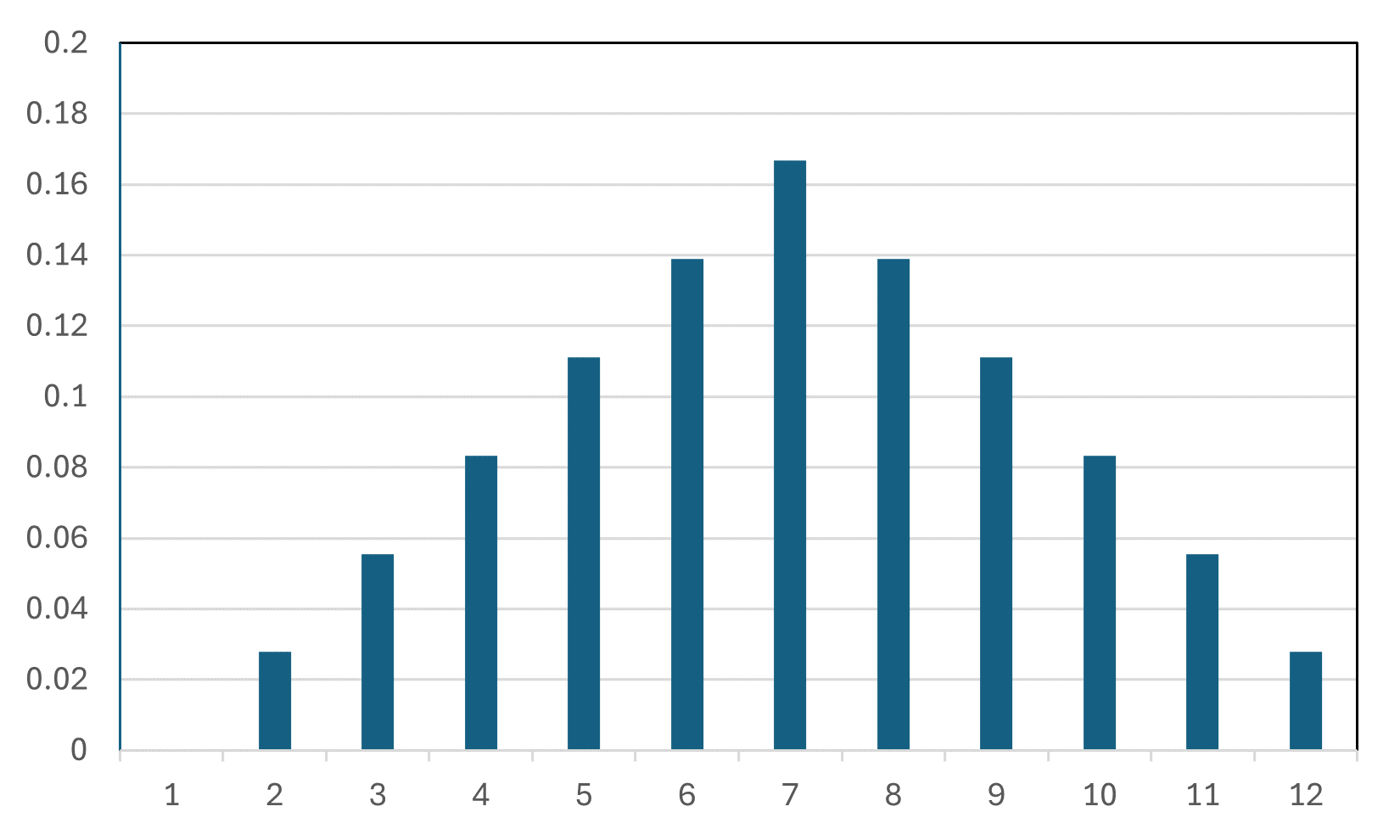
この時、横軸の数字が確率変数、縦軸が確率となります。
さらに、各確率変数の時の確率をつなげていくと、以下の様に表せて、これを確率分布と言います。
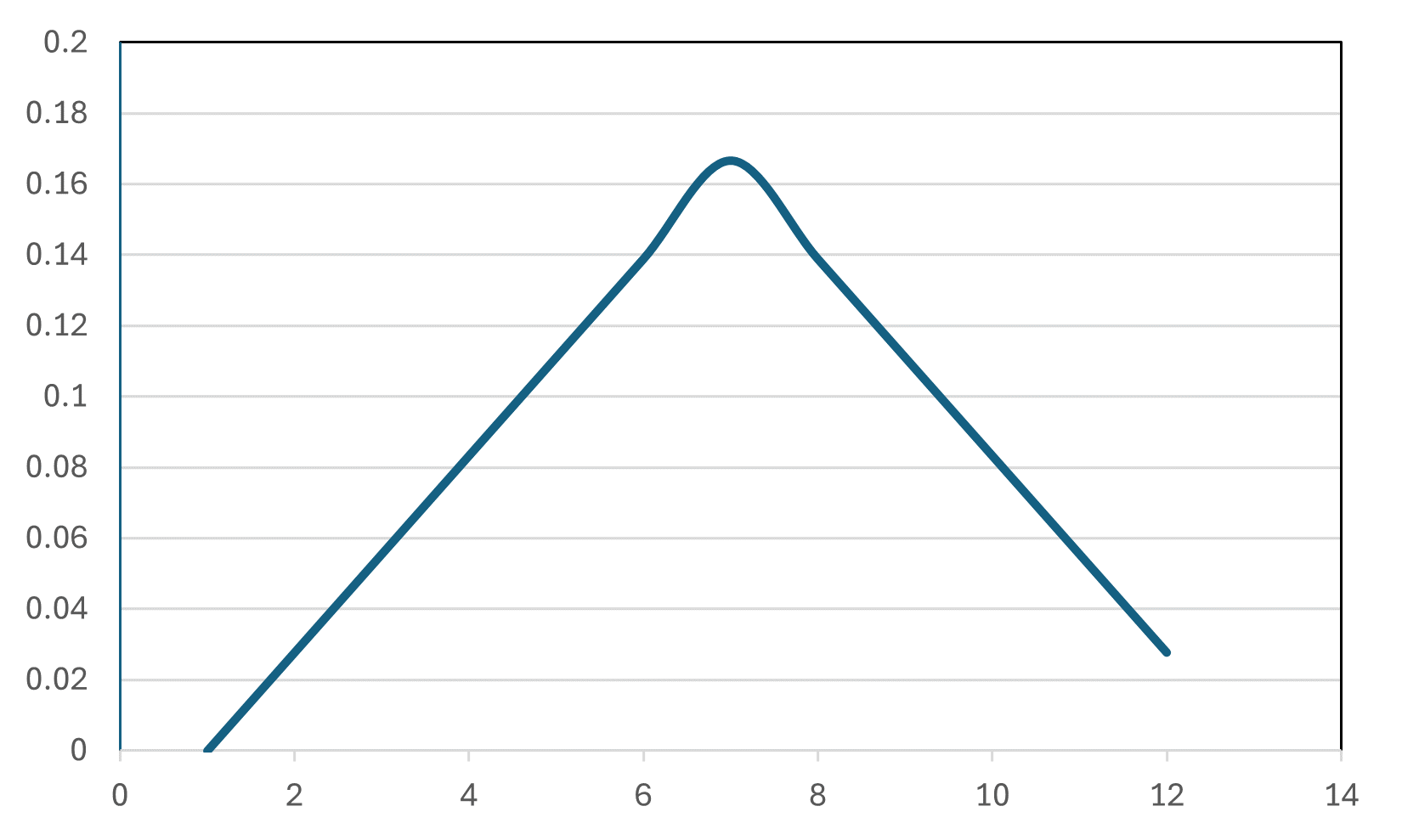
今回の例では、さいころの和を確率変数として扱いましたが、例えばコインの裏表の出る確率を調べたい場合、裏を0、表を1として確率変数を設定すると、その確率分布を描くことが出来ます。
このように、現象にも数字を割り当てられるのが、確率変数のメリットです。
標本調査と推定とは
テレビで「20代の平均摂取カロリー」の様なデータを見たことは無いでしょうか。
しかし、日本全国の20代全員にアンケートする事など不可能です。
その為、20代全体を調べたい集団として、その中の一部の20代に調査を行い、その結果から、20代全体の平均摂取カロリーを予測しているのです。
この時、調べたい集団（20代全体）を母集団、一部の20代を標本（サンプル）といい、このような調査を標本調査と言います。
また、母集団の特徴を与える数（平均や分散など）をまとめて母数（母平均や母分散などと表す）といいます。
推定や仮説検定では、母集団について調べる為に、標本を駆使して母数を探す訳です。
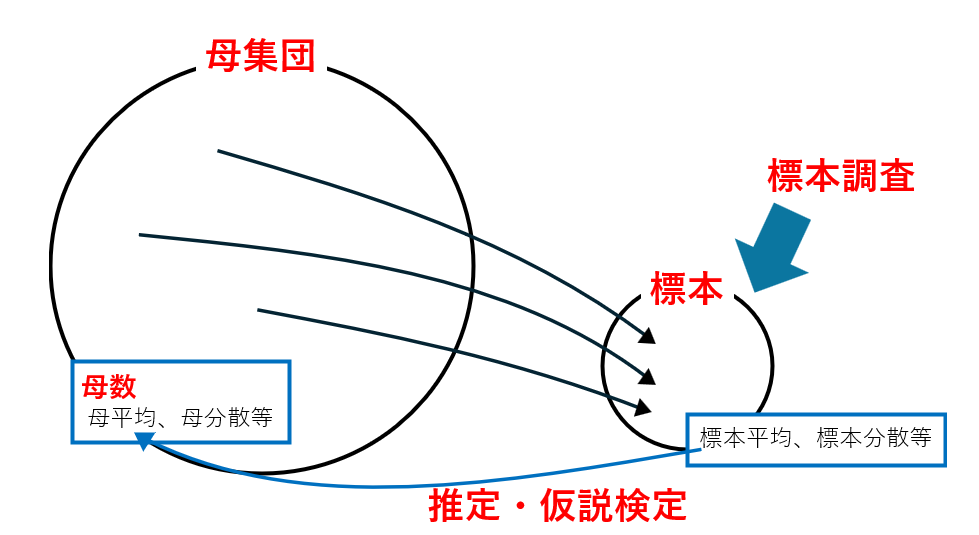
しかし、ここで、標本調査における平均（＝標本平均）が必ず母平均に等しくなるには、奇跡的にバランス良く標本が選ばれる必要があります。
しかし、標本に大食いの人が多く入っていたり、小食の人が多く入っている可能性は当然あり、標本平均が母平均に比べて高いのか低いのかは分かりません。
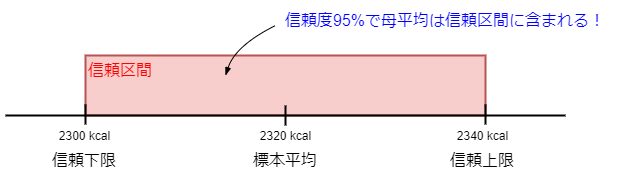
その為、例えば、標本平均2320kcalに対して、2300kcal~2340kcalの間等、標本平均を中心として区間を設けて、その区間に母平均が入っている事を考えます。
この方法を区間推定法と言います。
またこの時、2300kcal~2340kcalの様な区間を信頼区間といい、信頼区間の上限値（=2300kcal）及び下限値（=2340kcal）を信頼上限及び信頼下限と言います。
更に、この区間に母平均が入っている確率を信頼度と言います。
正規分布と標準正規分布とは
先ほど確認した、確率分布の様な分布曲線の形には、様々なものがあり、その中に、正規分布といったものがあります。
世の中には、この正規分布に従うとみなせるものが沢山あり、その特徴から、推定や検定において、多用されます。
まずは、正規分布の特徴について、下の画像を用いて説明していきます。
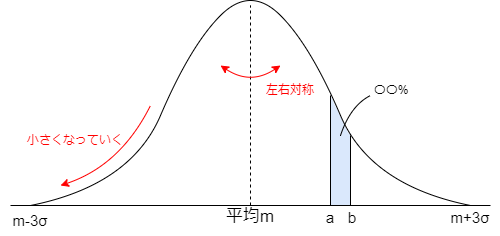
正規分布はこのように、平均に関して対称で、平均から離れる程小さくなっている様な概形をしています。
また、青の範囲の様に、曲線から垂線を下ろして出来た範囲の面積は、事象の結果が（今回ならaからbまでの）範囲に入る確率になり、曲線と横軸に囲まれた全体の面積は1になります。
ここで、正規分布の端がm±3σである事からも分かる様に、標準偏差σが大きい程、曲線は末広がりになります。
つまり、正規分布に従う時、平均と標準偏差が分かればどんなデータでも、任意の範囲における確率を求める事が出来る、という事です。
これに対し、正規分布の個々のデータから平均値を引き、標準偏差で割ると（＝基準化）、標準正規分布になります。
この基準化をすると、平均は0、標準偏差は1になります。
すると、先ほど平均値（中心）と標準偏差（端）に、確率変数と確率を左右されていた正規分布が、データの特徴に依存しなくなります。
これにより、全てのデータで同じ確率分布が使える為、仮説検定は、この標準正規分布を用いて行います。
正規分布と標準正規分布のExcelを用いた活用
正規分布に関するExcel関数
下図の青部分の様に、任意データx以下になる確率を累積確率といい、pで表します。
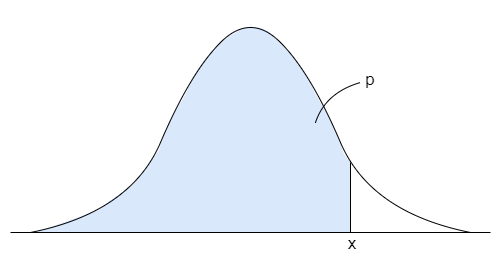
この時、任意データx(確率変数)に対する累積確率pは以下の関数を用いて計算する事が出来ます。
=NORM.DIST(x,平均,標準偏差,TRUE)
これを用いて、前章で用いたT小学校3年生の男子の身長を例に、累積確率pを求めてみると、次の様になります。
なお、Excelファイルの1ページ目のT小学校の男子の身長のデータから、平均身長は132.3cm、標準偏差は約9.32cmとしています。
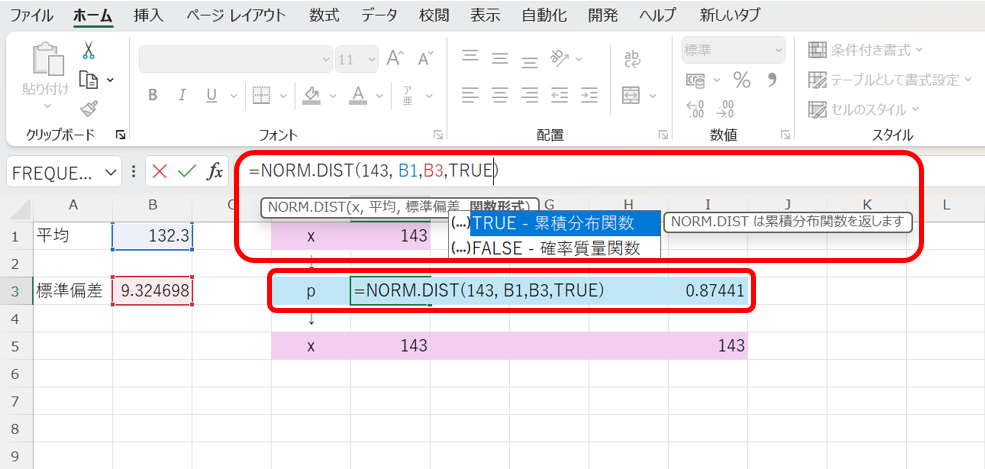
すると、以下の様に、143cmの累積確率が約87.4%と求まりました。
更に、累積確率pに対応するデータの大きさは、以下の関数を用いて計算する事が出来ます。
=NORM.INV(累積確率,平均,標準偏差)
これを用いて、先ほど求めた累積確率を元のデータに戻してみましょう。
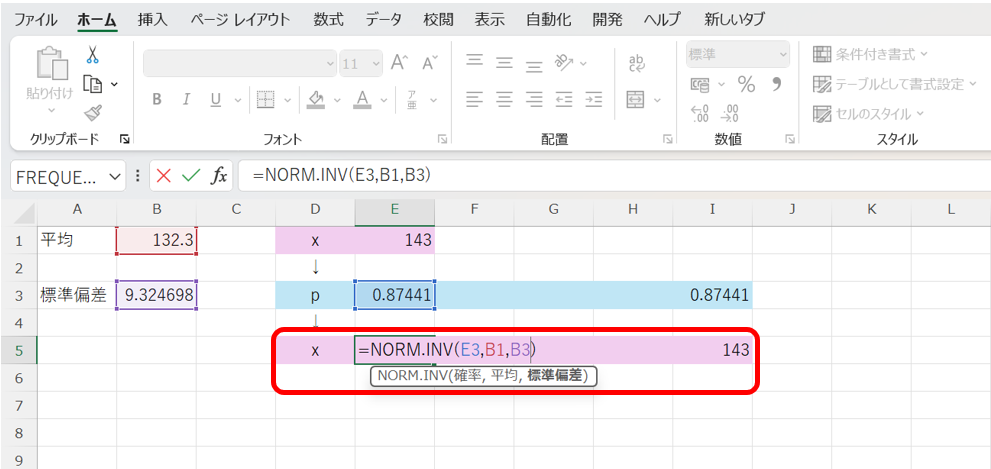
上の画像から、正常に元のデータに戻り、累積確率が対応するデータxの値が計算できました。
標準正規分布に関するExcel関数
標準正規分布において、任意の基準値z（=基準化されたデータの値）に対する累積確率pは以下の関数を用いて計算する事が出来ます。
=NORM.S.DIST(z, TRUE)
これを用いて基準値1.96の時の累積確率を求めると、以下の様になります。
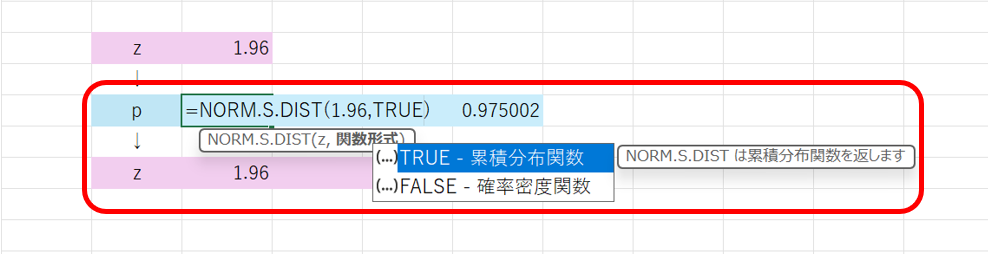
次に、標準正規分布において、任意の累積確率pに対応する基準値zは以下の式で計算できます。
=NORM.S.INV(確率)
これを用いて先ほど求めた累積確率を基準値に直すと、以下の様になります。
これより、正常に元のデータに戻り、累積確率に対応す基準値zが計算できました。
正規分布の関数を実際に使ってみよう
応用問題1
Excelファイル2ページ目のT小学校3年生の男子の身長のデータから、身長125cm以上130cm以下の生徒が何%いると思われるかを計算してみましょう。
また、その生徒は何人だと予想出来るでしょうか。
（ヒント：130cmの累積確率と125cmの累積確率は…?）
125cm以上130cm以下の生徒の確率は、
(130cmの累積確率)ー(125cmの累積確率)
で求める事が出来ます。
その為、以下の様にして計算します。
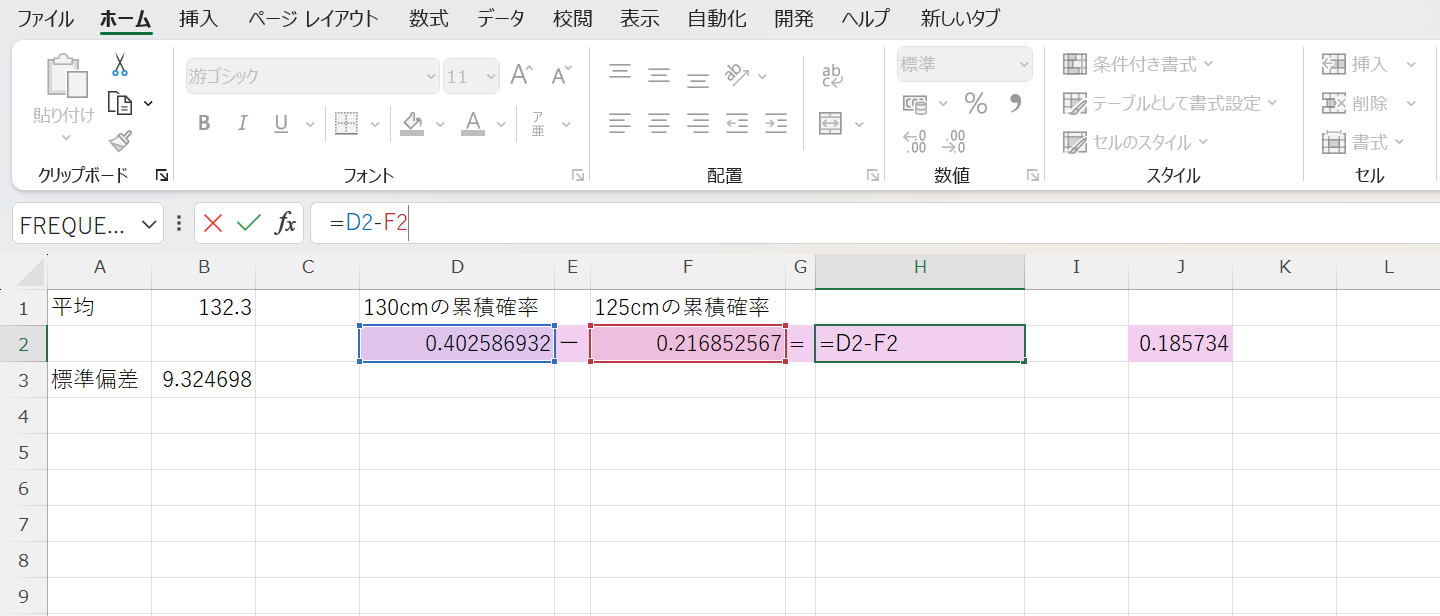
よって、これより、身長125cm以上130cm以下の生徒は約18.6%いると思われます。
そして、今回のデータ数が、100個であることから、18.6人いると思われます。
このように、正規分布は生徒の数を数えずとも、計算で生徒数や確率を求める事が出来ます！
応用問題2
Excelファイル2ページ目の、-3から3まで0.1間隔で並んだ数値を使って、標準正規分布の概形を出力してみましょう！
（ヒント：先程の関数の関数形式について、TRUEなら累積確率、FALSEなら確率密度関数(＝数値に対応する確率の値)が出力されます。）
関数の関数形式について、FALSEにすると、確確率密度関数(＝数値に対応する確率の値)が出力されるので、各数値に対して、
=NORM.S.DIST(z, FALSE)
として実行し、数値と計算結果をグラフにする事で、標準正規分布を得る事が出来ます。
まず、数値から確率密度関数を算出します。
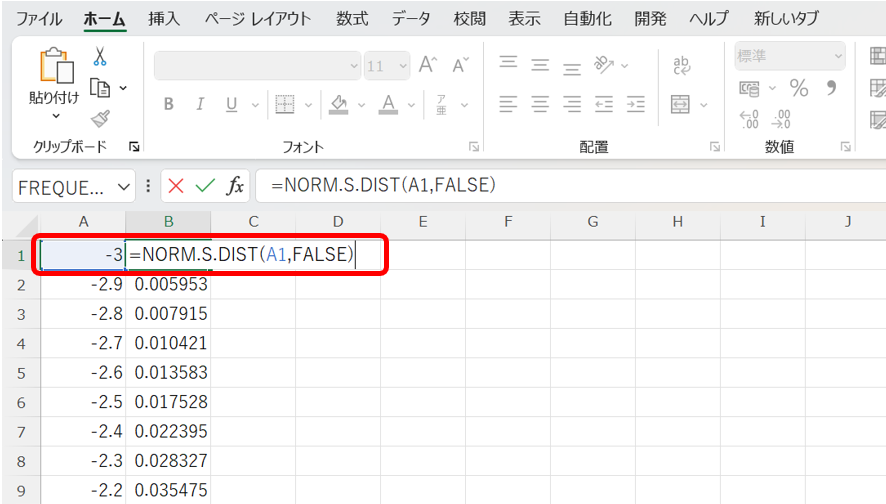
次に、この2つのデータをグラフにします。
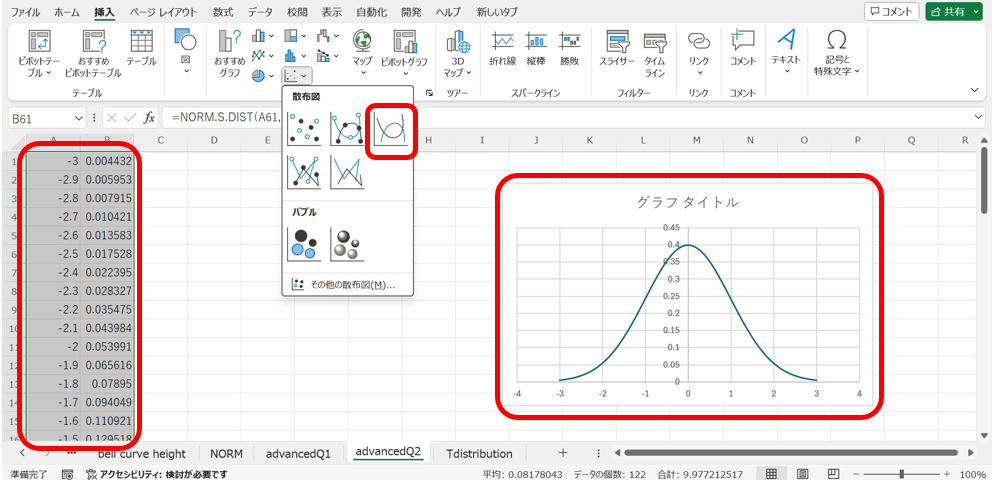
これで、標準正規分布の概形が出力できました。
「データが正規分布に従っているかどうかなんて、母集団が分からないんだから分からないじゃないか」
初めてこの分野の勉強をした時の自分は、こう思っていたため、正規分布に不信感しかありませんでした（笑）。
しかし、勿論、正規分布に従っているかどうかを調べる方法はあります。
それが、正規確率プロットです。
これに関しては後の回帰分析の章で説明していますので、是非読んでみて下さい！
まとめ
今回のExcelによる統計解析講座第8章では、仮説検定に入る前段階として、確率分布、正規分布や標本調査について解説してきました。
これらは、統計学及びデータ分析を学ぶ上で、避けては通れない道なので、是非しっかり身に付けていってほしいです！
また、次章では、t検定とz検定を用いた、母平均と母比率の仮説検定について学んでいきます。
今回学んだ内容を早速使うので、今回学んだ内容を、身に付ける為にも出来れば連続して読んでいただけると嬉しいです！
