【1分でわかる】機械学習の勾配法の概要と仕組みを丁寧に解説

「AIはどのようにして学習を進めるのか」と疑問に思ったことはありませんか？

実は、機械学習を支える最も重要なアルゴリズムが勾配法です。これは数学の微分法に基づいて誤差を少しずつ削減させる技術ですが、仕組みと種類、複数のアルゴリズムを知ることで、適切な機械学習の実装ができるようになります。

勾配法とは

勾配法の仕組み

簡単に言うと、勾配は関数の傾きや変化率のことで、最小値または最大値の方向を指し示す重要な値です。

勾配法はこの勾配を活用して関数の極小値や極大値を見つけるための最適化手法です。基本的に、現在の位置から勾配の方向に一定の距離（学習率）だけ進み、新しい位置で同様の操作を繰り返すことで、反復的な調整が実行されて機械学習のモデル学習が可能となります。

勾配法の種類

勾配法にはいくつかのアルゴリズムが存在します。代表的な3つを見てみましょう。

• バッチ勾配法
• ミニバッチ勾配法
• 確率的勾配法

バッチ勾配法では、データセット全体を一度に使用して勾配を計算し、パラメータを更新します。全体のデータを考慮するため、収束は安定していますが、計算コストが高いという特徴があります。

次に、ミニバッチ勾配法はデータセットをランダムに選んだ小さなバッチごとに勾配を計算し、パラメータを更新します。その結果、計算効率が向上し、バッチ勾配法と比べて一般的にメモリの使用量が削減されます。

最後に確率的勾配法は、データセットからランダムに1つのデータを選び、そのデータに基づいて勾配とパラメータを更新します。この手法は計算効率が非常に高い反面、ノイズの影響を受けやすく、収束が不安定な場合があるため、注意しましょう。

勾配法の数学的背景

偏微分

数学には微分と呼ばれる関数の傾きを調べる方法がありますが、特に複数の変数を持つ多変数関数の傾きを調べるものを偏微分と言います。一般的な微分法とは異なり、偏微分法の特徴は指定した変数の方向に対して傾きを得るためにその他の変数を固定して計算することです。

実は機械学習におけるニューラルネットワークは入力が複数ある多変数関数で、偏微分によるアプローチが主流です。

連鎖律

まずは合成関数について理解することから始めましょう。簡単に言うと、2つの関数を順番に値を変換する全体を合成関数といい、この微分は逆向きに計算することで微分を連鎖的に求められます。

複雑な関数をいくつかの関数が合わさった合成関数であると捉えて、逆の順番に微分の値を調べることが有効です。このような連続的な鎖のことを連鎖律と呼びます。

誤差逆伝播法

なぜ機械が学習能力を得たかを説明する上で最も重要な概念である誤差逆伝播法をご紹介します。

多変数のパラメータを持つニューラルネットワークも入力から出力を得る関数であり、その誤り具合を示す誤差関数をパラメータの更新により調べて最小化することが機械学習における学習です。

この最小化には関数の傾きである勾配を偏微分によって求めることが必要です。具体的には、出力と正解の差から逆算して、パラメータのズレを改善していきます。

Pythonでの実践例

基本的に機械学習の実装ではPyTorchやTensorFlowなどのライブラリが用いられますが、勾配法について理論から理解するために標準ライブラリを中心に勾配法を体験してみましょう。

勾配法の基本

まずは勾配法の効果を知るために、簡単な二次関数を目的関数として最小化してみましょう。以下のコードでは行列の計算にnumpyライブラリを、結果の可視化にmatplotlibライブラリを利用しています。

import numpy as np
import matplotlib.pyplot as plt

# 目的関数
def target_function(x):
    return x**2 + 2*x + 1

# 目的関数の導関数
def gradient(x):
    return 2*x + 2

# 勾配法の実装
def gradient_descent(learning_rate, iterations):
    # 初期値を設定
    x = 0.0
    x_history = [x]
    y_history = [target_function(x)]

    # 収束まで繰り返す
    for _ in range(iterations):
        # 勾配を計算
        grad = gradient(x)

        # パラメータを更新
        x = x - learning_rate * grad

        # 履歴を保存
        x_history.append(x)
        y_history.append(target_function(x))

    return x_history, y_history

# パラメータの設定
learning_rate = 0.1
iterations = 10

# 勾配法の実行
x_history, y_history = gradient_descent(learning_rate, iterations)

# 結果の可視化
x_vals = np.linspace(-3, 1, 100)
y_vals = target_function(x_vals)

plt.plot(x_vals, y_vals, label='f(x) = x^2 + 2x + 1')
plt.scatter(x_history, y_history, color='red', label='Gradient Descent Steps')
plt.title('Gradient Descent Visualization')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.show()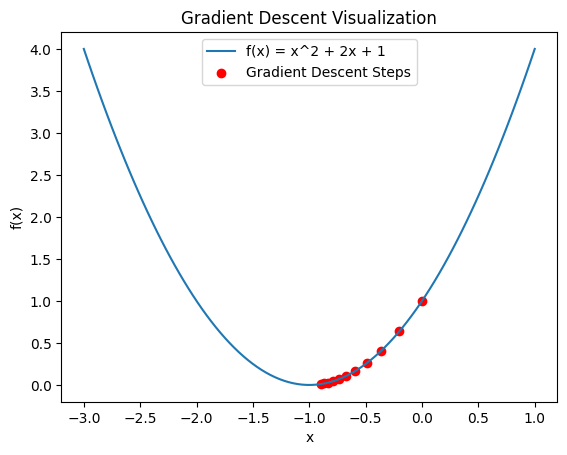

実行すると関数と勾配法による最小化の過程が観察できます。今回は変数の数が1つなので簡単に最小値が発見できますが、実際の機械学習では非常に複雑な目的関数を最適化します。

ニューラルネットワーク

ニューラルネットワークにおける勾配法を理解するため、シンプルなロジスティック回帰を実装してみましょう。損失関数は交差エントロピー誤差で実装され、活性化関数はシグモイド関数を利用します。

import numpy as np
import matplotlib.pyplot as plt

# シグモイド活性化関数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 目標の関数：ロジスティック回帰
def logistic_regression(x, w, b):
    return sigmoid(np.dot(x, w) + b)

# ロス関数：クロスエントロピー
def cross_entropy(y_true, y_pred):
    epsilon = 1e-15
    y_pred = np.clip(y_pred, epsilon, 1 - epsilon)
    return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

# 勾配計算
def compute_gradient(x, y_true, y_pred):
    dw = np.dot(x.T, (y_pred - y_true))
    db = np.sum(y_pred - y_true)
    return dw, db

# 勾配法でパラメータ更新
def gradient_descent(x, y_true, w, b, learning_rate, iterations):
    loss_history = []

    for _ in range(iterations):
        # 予測を計算
        y_pred = logistic_regression(x, w, b)

        # ロスを計算
        loss = np.mean(cross_entropy(y_true, y_pred))
        loss_history.append(loss)

        # 勾配を計算
        dw, db = compute_gradient(x, y_true, y_pred)

        # パラメータを更新
        w = w - learning_rate * dw
        b = b - learning_rate * db

    return w, b, loss_history

# データの生成
np.random.seed(42)
x = np.random.randn(100, 2)
w_true = np.array([2, -3]).reshape(-1, 1)
b_true = 1.5
y_true = (sigmoid(np.dot(x, w_true) + b_true) > 0.5).astype(int)

# パラメータの初期化
w_init = np.random.randn(2, 1)
b_init = np.random.randn()

# パラメータの学習
learning_rate = 0.01
iterations = 1000
w_learned, b_learned, loss_history = gradient_descent(x, y_true, w_init, b_init, learning_rate, iterations)

# 結果の可視化
plt.plot(loss_history)
plt.title('Training Loss over Iterations')
plt.xlabel('Iterations')
plt.ylabel('Cross Entropy Loss')
plt.show()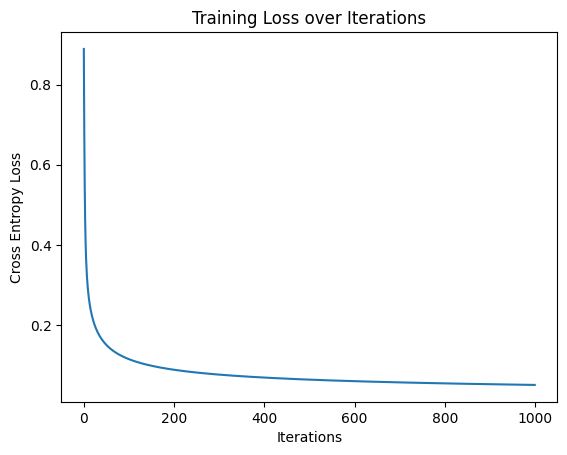

このグラフは機械学習で一般的に見られ、誤差の変化を直感的に理解できますね。正解の重みを事前に定義しており、それを見つけるような訓練が記載されています。

勾配法の注意点

過学習の防止

訓練用のデータに過剰に適合してしまい、テストデータでは十分なスコアが得られない状態を過学習と言います。

受験勉強で例えてみましょう。

受験生はある参考書を何周も反復的に学習した結果、問題を見るだけで答えが思い浮かぶ状態になりました。しかし、試験本番では当然参考書とは異なるテスト問題が出題され、合格に必要な点数が得られないことになります。

つまり、参考書という訓練データに過剰適合した結果、試験問題というテストデータで十分なスコアが得られない過学習の状態です。機械学習においても過学習を防止するために正則化やドロップアウトなどの手法が用いられます。

最適化手法の選択

最適化手法にはいくつかの種類があり、代表的アルゴリズムをいくつか見てみましょう。

• Gradient Descent
• Momentum
• RMSProp
• Adam

最急降下法（Gradient Descent）は最も基本的な最適化アルゴリズムで、勾配に基づいて逐次的にパラメータを更新します。これを発展させた確率勾配降下法（SGD, Stochastic Gradient Descent）やミニバッチSGDは、それぞれ学習データは1ずつとミニバッチと呼ばれるデータをいくつか分けたものを利用します。

次に、モーメンタム（Momentum）は移動平均を利用してより速く収束へ向かうことのできるアルゴリズムです。移動平均は値の急激な変化に対応でき、パラメータ調整の激しい振動を緩和させる特徴があります。

一方、RMSPropは学習率の調節によって振動を抑制します。モーメンタムと似た性質を持ちますが、振動の大きい部分で学習率を小さくして影響を抑える効果が特徴的です。

最後に、汎用的に利用される最適化アルゴリズムであるAdamをご紹介します。基本的にこの最適化手法を選択することで学習速度と安定性を高められ、多くのケースで効果的です。

まとめ

勾配法は機械学習を実現したアルゴリズムであり、最適化の速度と安定性を高めるための工夫が考案されてきました。具体的なPythonでの実装例を通して、より一層勾配法に対する理解が深められると、人工知能の中身を理解できたと言えますね。

本記事では最適化手法についてご紹介しましたが、ロジスティック回帰モデル以外にも数多くのモデルが開発されていますので、気になる方は調べてみましょう。