連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第18章では、「分散分析」について解説します。
分散分析のアイディアや分散分析の手順を解説しています。
初学者も理解しやすいように丁寧に解説しているので、ぜひ最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
分散分析
分散分析とは
分散分析は、3つ以上の集団間に平均値に差があるかを検定する手法です。
集団のことを「群」と呼ぶ場合が多いです。
分散分析は、「Analysis of Variance」から「ANVOA」と呼ばれることもあります。
分散ではなく、平均について検定していることに注意しましょう。
母平均の検定といえば、分散が既知の場合の正規分布を利用した検定と、分散が未知のt分布を利用したt検定がありました。
この2つの検定の理解に不安がある方は、合わせて下記の記事をご覧ください。

この2つの検定は、分散分析と同様に「平均値の差」についての検定をしていましたが、2集団間に限られていました。
一方、分散分析は、3集団以上の「平均値の差」について検定を行うことができます。
したがって、分散分析を利用すれば「異なるクラス(1組、2組、3組)」、「異なる都道府県(47県)」など幅広い集団の検定が可能になります。
分散分析のイメージ
分散分析の具体的な方法に入る前に、分散分析の考え方のイメージについて解説していきます。
分散分析は、集団(群)の平均値のデータに分散の情報を追加し、集団間の差を捉えています。
具体例を用いて、理解していきましょう。
例題
ある学校の生徒についての調査では、数学と英語の点数がそれぞれデータ1とデータ2で記録されました。
3つの異なるクラス
- 1組:青色
- 2組:赤色
- 3組:緑色
間での平均点の違いを検討しました。
平均点がクラス間で差があれば、「先生の教え方に問題があった」や「クラス編成に問題があった」と分析に繋げることができます。
分散分析の考え方を用いて、クラス間の平均点に差があるかを調べてみましょう。
下記の図は、データ1(数学の点数)とデータ2(英語の点数)のクラスごとの平均点を表しています。
どちらのデータも
- 1組:平均点数が最も低い
- 2組:平均点数が最も高い
- 3組:平均点数が真ん中
と分かります。
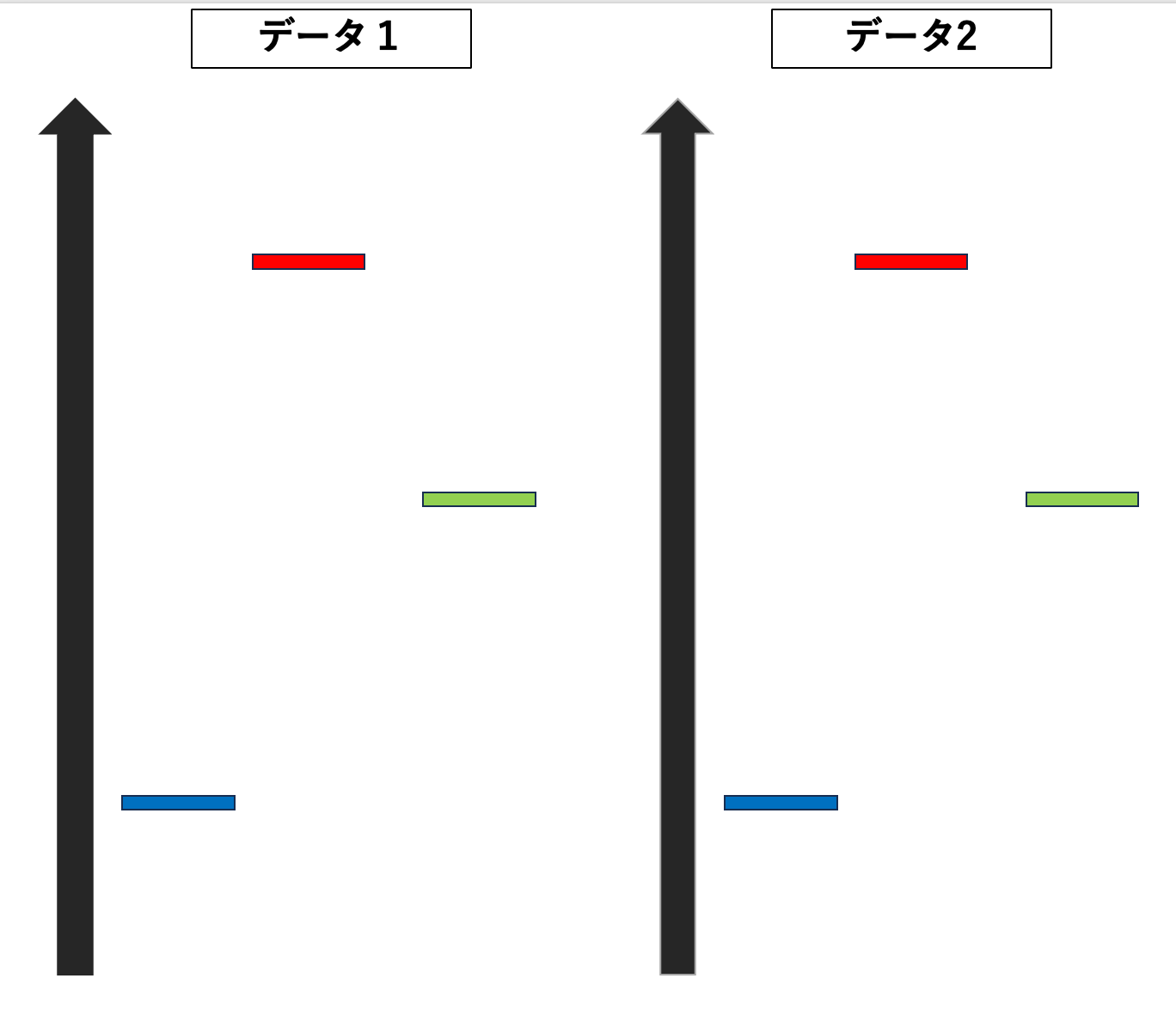
では、ここに分散(散らばり)の情報を追加してみましょう。
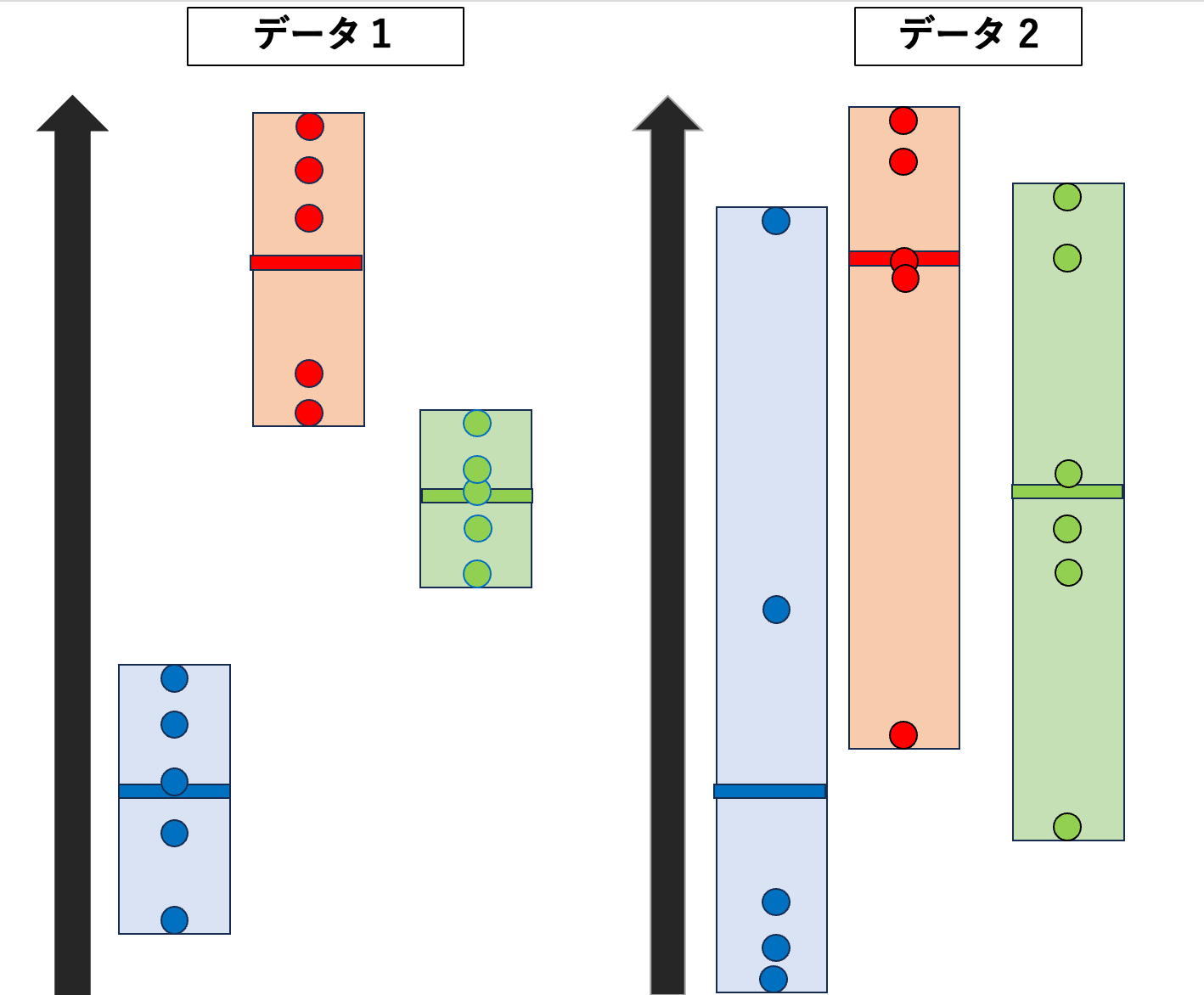
データ1とデータ2でそれぞれのクラスの平均点は変わりませんが、データの印象は大きく変わった様に感じると思います。
データ1は、集団(群)内で点数がまとまっており、グループ間での違いが明らかに表れています。
したがって、データ1では「集団間で平均点に差がある」と言えるでしょう。
一方、データ2では、集団(群)内でばらつきが大きく、グループ間の差が明らかではない様に見えます。
このように、分散分析は群間と群内の散らばり具合を比較して、グループ間の平均値に差があるかを検証します。
分散分析の手順
では、実際に分散分析を行なっていきましょう。
分散分析は以下の手順で行います。
- Step1:群間平方和、郡内平方和を求める
- Step2:自由度を求める
- Step3:平均平方を求める
- Step4:F値を求める
- Step5:F値・F分布を使って検定する
分散分析は上記の手順に基づいて、下記の分散分析表を埋めます。
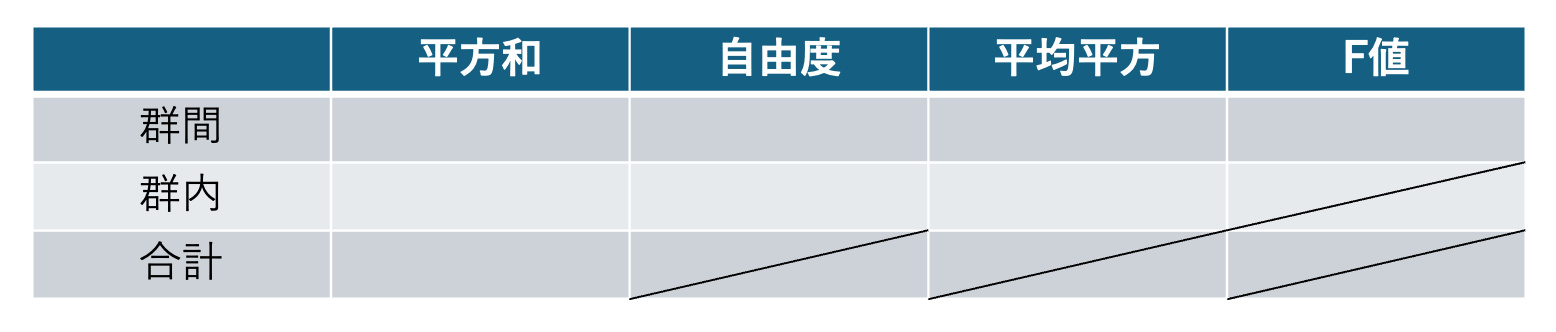
以下の例題を用いて、解説していきます。
例題
国際的な健康調査を行っています。
ある研究では、3つの異なる国(国A、国B、国C)からの男性の身長データを収集しました。
このデータを使用して、これらの国の男性の平均身長に違いがあるかどうかを検討したいと考えています。
以下は、各国からの3人の男性の身長データです。
| A国 | B国 | C国 |
| 170 cm | 169 cm | 184 cm |
| 178 cm | 176 cm | 181 cm |
| 168 cm | 168 cm | 172 cm |
このデータを使用して、3つの国の男性の平均身長に統計的に有意な違いがあるかどうかを検定するために、分散分析(ANOVA)を実行してください。
有意水準は0.05とします。
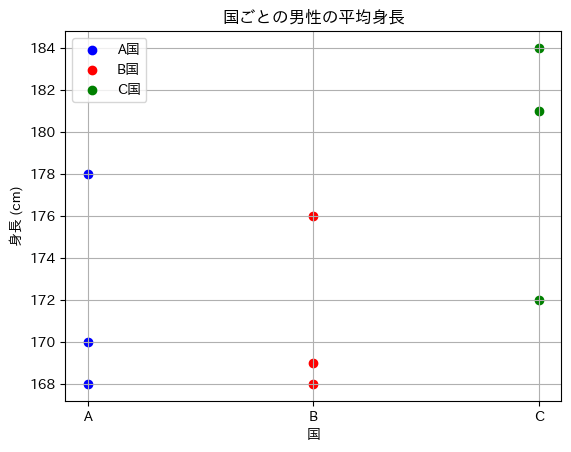
分散分析に入る前に、帰無仮説と対立仮説について確認しておきましょう。
- 帰無仮説:各国の男性の平均身長は等しい
- 対立仮説:少なくとも1つの国の男性の平均身長は他と異なる
と設定できます。
では、stepごとに進めていきましょう。
Step1:群間平方和、群内平方和を求める
まず、群間平方和と群内平方和の用語について説明します。
群間平方和とは、全体平均と全サンプルとの差を2乗したものの総和です。
群間平方和は、データ全体の分散を求める際に「nで割らない」と考えると理解しやすいかもしれません。
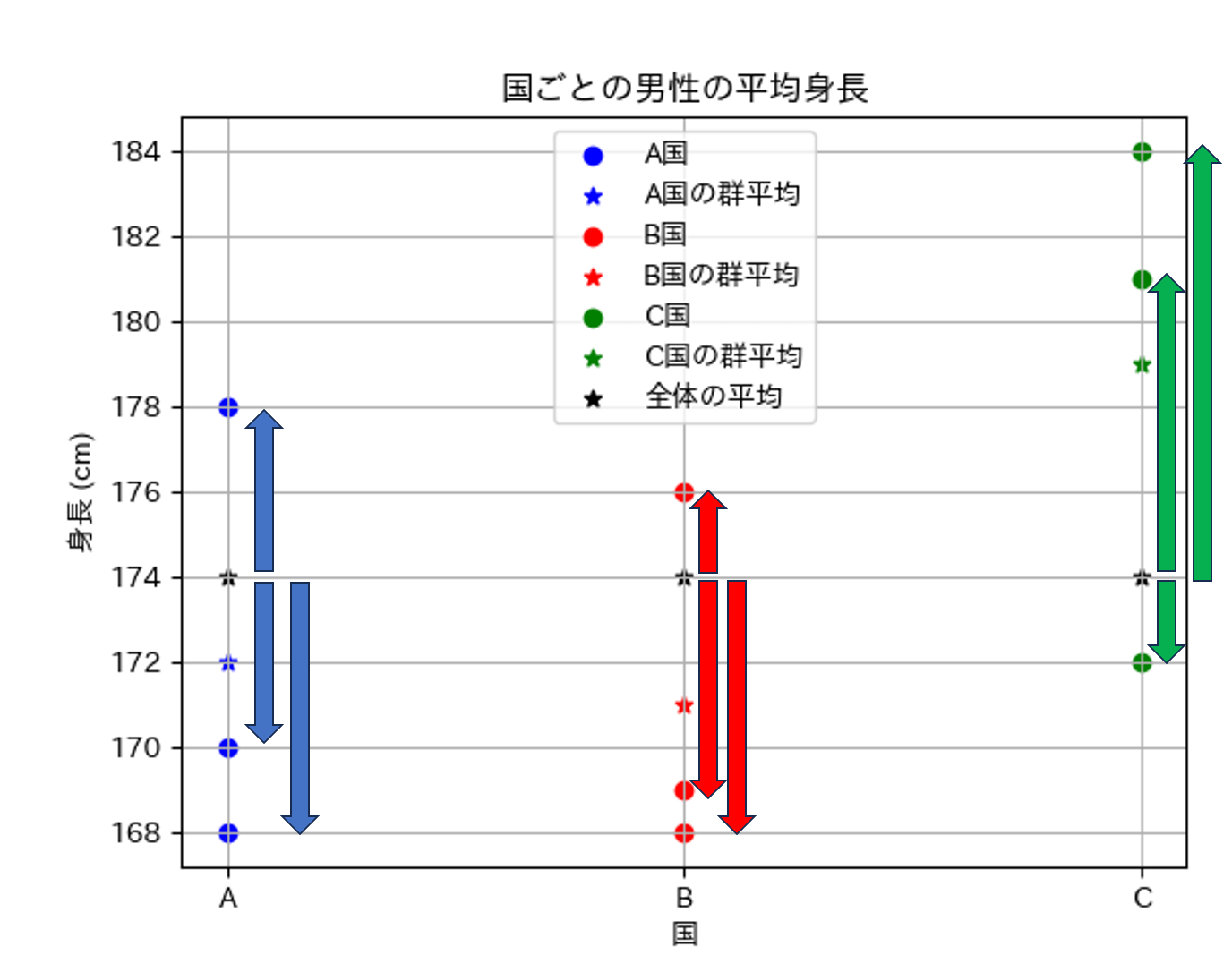
実際に、群間平方和を求めていきましょう。
まず、データ全体の平均uを求めます。
$$ u = \frac{170 + 178 + \dots + 172}{9} = 176 $$
よって、群間平方和SSBは
$$
\begin{align*}
SSB &= (170 – 176)^2 + (178 – 176)^2 + \dots + (172 – 176)^2 \\
&= 286
\end{align*}
$$
となります。
次に、群内平方和を解説していきます。
群内平方和とは、群平均とその群のサンプルとの差を2乗したものの総和です。
群内平均は、その群の分散を求める際に「nで割らない」と考えると理解しやすいかもしれません。
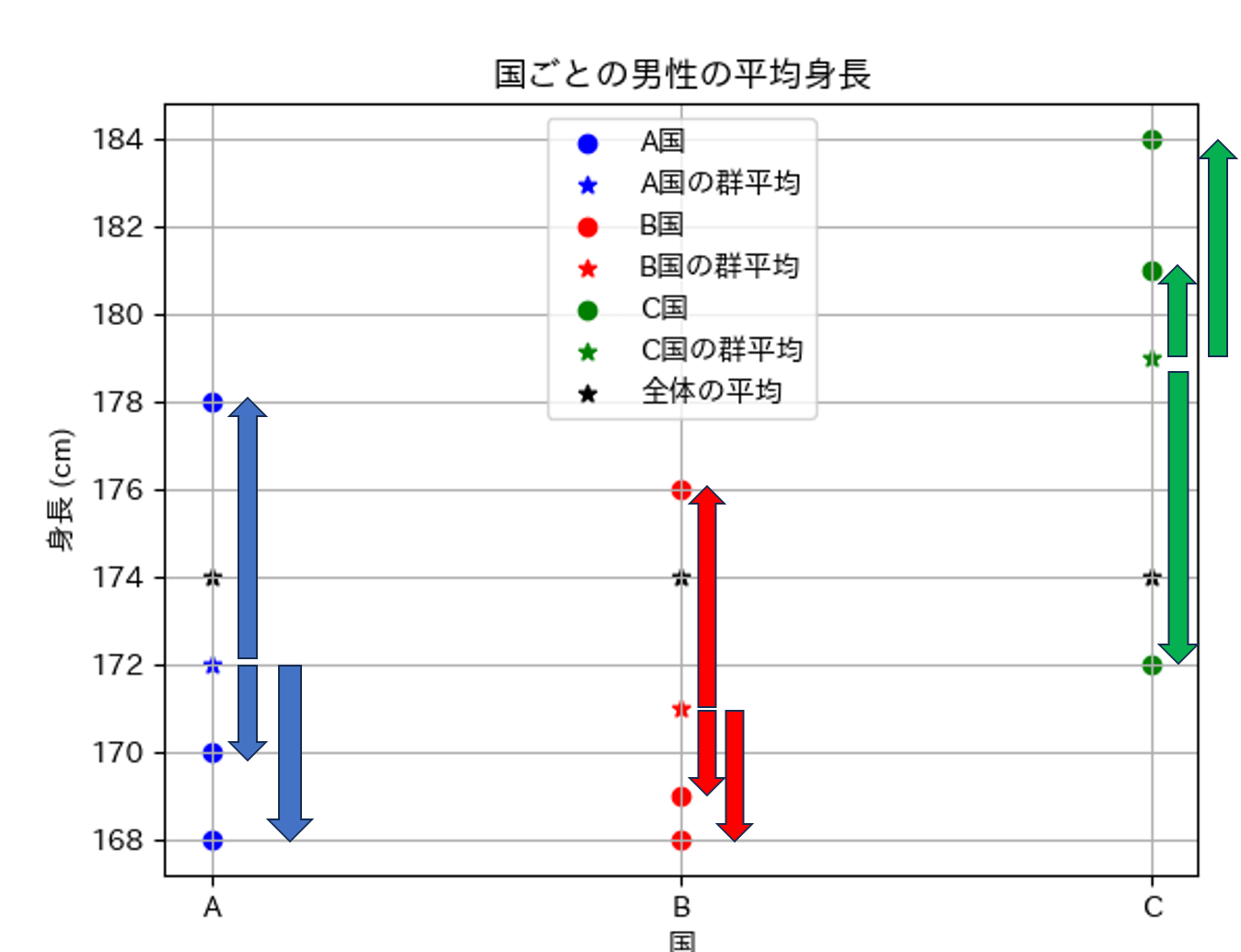
実際に、群内平方和を求めていきましょう。
まず、それぞれの群平均\(u_A\)、\(u_B\)、\(u_C\)を求めます。
$$ u_A = \frac{170 + 178 + 168}{3} = 172 $$
$$ u_B = \frac{169 + 176 + 168}{3} = 171 $$
$$ u_C = \frac{184 + 181 + 172}{3} = 179 $$
よって、群内平方和SSWは
$$
\begin{align*}
SSW = &(170 – 172)^2 + (178 – 172)^2 + (168 – 172)^2\\
&(169 – 171)^2 + (176 – 171)^2 + (168 – 171)^2\\
&(184 – 179)^2 + (181 – 179)^2 + (172 – 179)^2\\
= & 56 + 38 + 78 \\
= & 172
\end{align*}
$$
となります。
したがって、平方和の合計SSTは
$$
\begin{align*}
SST &= SSB + SSW\\
&= 286 + 172\\
&= 458
\end{align*}
$$
となります。
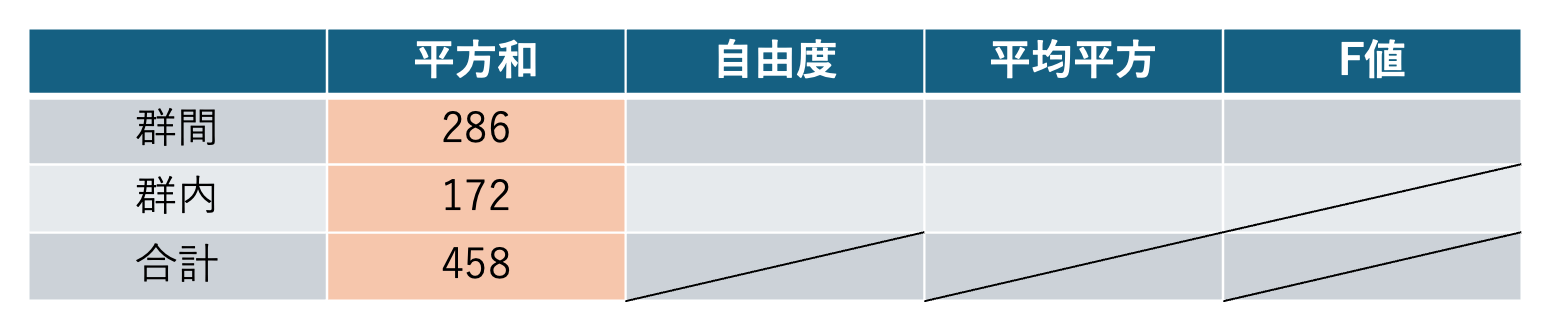
Step2:自由度を求める
次に群間と群内の自由度を求めます。
群間の自由度は以下の式で求めることができます。
群間の自由度:「カテゴリー数」- 1
今回の問題の場合、カテゴリー数は「3」なので、群間の自由度は「2」となります。
一方、群内の自由度は以下の式で求めることができます。
群内の自由度:「サンプル数」ー「カテゴリー数」
今回の問題の場合、「サンプル数」は「9」、カテゴリ数は「3」なので、群内の自由度は「6」となります。
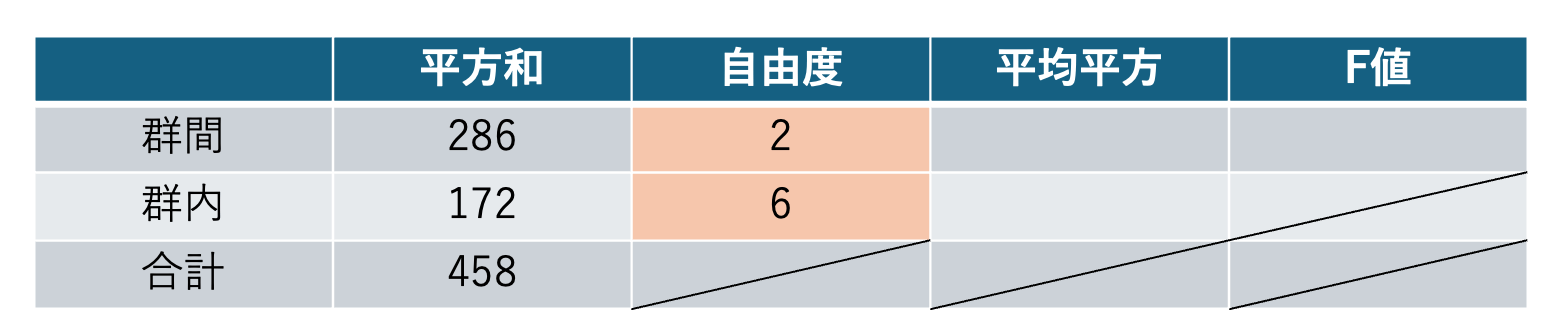
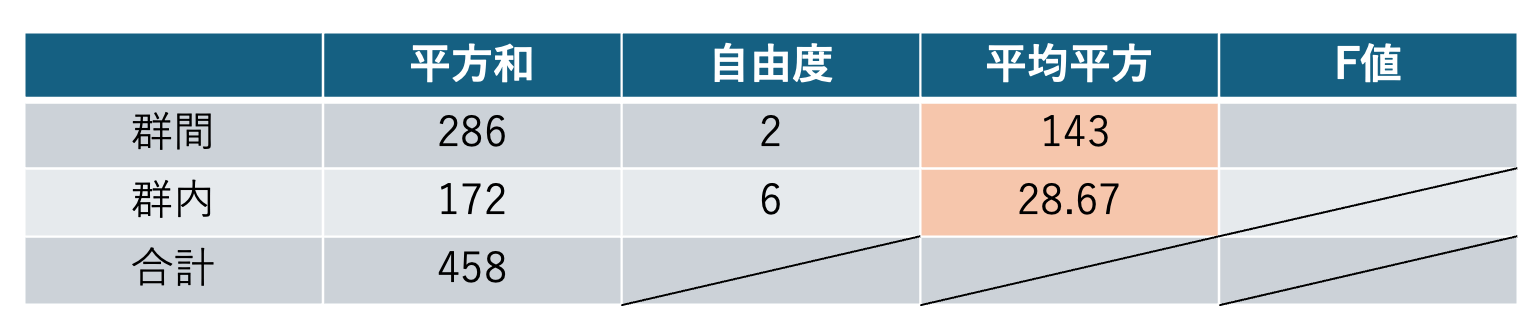
Step4:平均平方を求める
次に、平均平方和を求めます。
平均平方和は、平方和を自由度で割ったものです
したがって、群間の平均平方は
$$ \frac{286}{2} = 143 $$
となります。
群内の平均平方は
$$ \frac{172}{6} \simeq 28.67 $$
となります。
step4:F値を求める
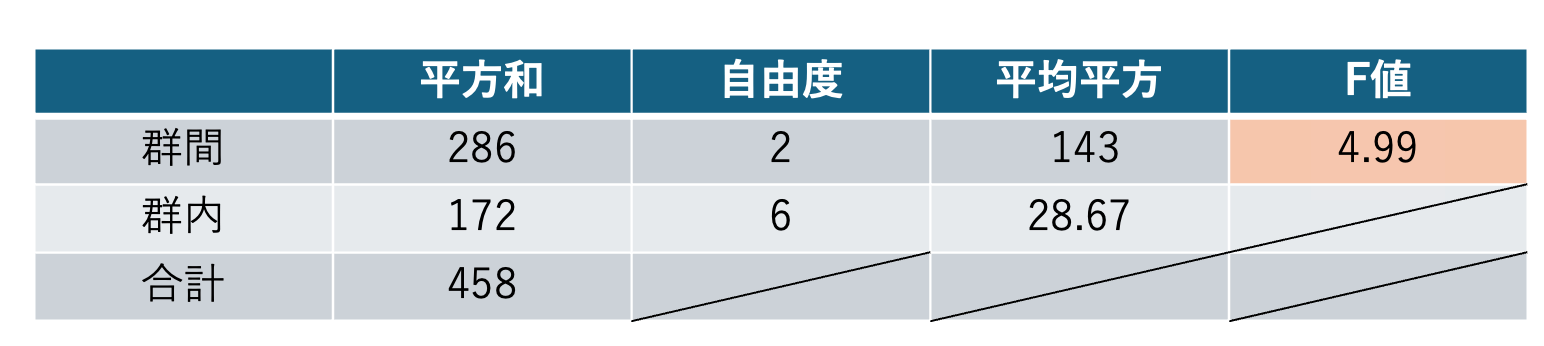
次に、F値を求めます。
F値は、「群間平均平方」/「群内平均平方」で求めます。
したがって、F値「f」は
$$ f = \frac{143}{28.67} \simeq 4.99 $$
となります。
step5:F値・F分布を使って検定する
F値・F分布は以下の記事で詳しく解説しているので、理解に不安がある方は合わせてご確認ください。

分散分析の場合、F値は自由度(群間自由度、群内自由度)のF分布に従います。
今回の問題では、群間自由度は「2」、群内自由度「6」なので、F値は自由度(2,6)のF分布に従います。
有意水準は5%と与えられているため、計算サイトやf分布表を用いて上側5%\(p_+\)を求めると
$$ p_+ = F_{0.05}(2,6) \simeq 5.14 $$
となります。
よって、棄却域は
$$ 5.14 < F $$
となります。
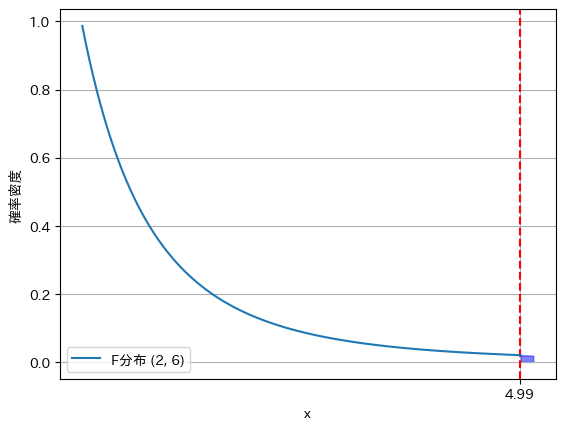
棄却域とF値の実現値fを比べると、fが棄却域外にあるため、帰無仮説\(H_0\)を受容・対立仮説\(H_1\)を棄却します。
したがって、「各国の男性の平均身長は等しい」という結論が得られました。
このように分散分析は、手順に従って分散分析表を作り、F分布を使って検定を行います。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
分散分析の弱点
上記で行なった様に、分散分析を利用すれば、3集団間以上で「平均値に差があるか」を検定することができました。
そのため、分散分析により仮設検定を行える範囲が非常に広くなりました。
しかし、分散分析にも弱点ががあります。
分散分析では、「平均値に差があるか」しか分かりません。
更に言えば、「平均値に差がある」という結論が出ても、「どこに差があるか」を知ることはできません。
「どこに差があるか」を分析したい場合は、多重比較や回帰分析など別の分析手法を利用しましょう。










