連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第19章では、「回帰分析」について解説します。
初学者も理解しやすいように丁寧に解説しているので、ぜひ最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
回帰分析とは
『回帰分析』は、予測したい変数を他の変数で表した式を求めることです。
例えばあなたがアイスクリーム屋を経営していて、1日の売り上げ\(y\)を予測したいと考えたとします。
このとき1つの方法として、「1日の売り上げ\(y\)を、その日の平均気温(\(x\))を用いた式で表す」という手段考えられます。
このようにして求めた式\(y=f(x)\)のことを『回帰式』といい、回帰式を求めることを『回帰分析』と言います。
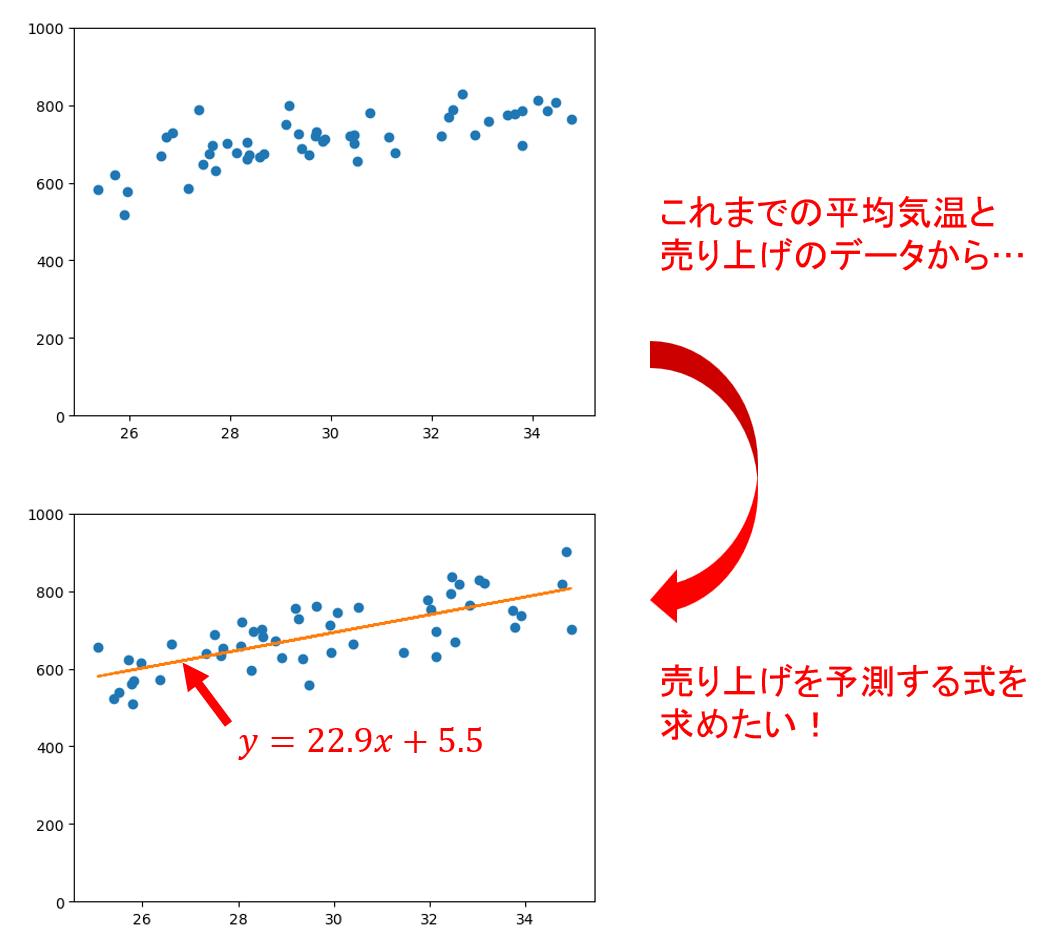
回帰分析にはさまざまな種類があり、今紹介した方法は『単回帰分析』に分類されます。
本記事ではこのほかに『重回帰分析』および回帰式の評価に使える『決定係数』について解説します。
目的変数と説明変数
回帰分析を行う上で頻繁に登場する言葉として『目的変数』と『説明変数』があります。
それぞれの意味は以下の通りです。
- 『目的変数』:分析の対象となる変数。他の変数の影響を受けた結果を表す。
- 『説明変数』:何かの原因となる変数。目的変数を説明する。
もっと分かりやすく言うと、『目的変数』は予測したい変数で、『説明変数』はその原因となる変数です。
先ほどの例に当てはめると、1日の売り上げ\(y\)が『目的変数』、その日の平均気温\(x\)が『説明変数』に当たります。
単回帰分析と重回帰分析
『単回帰分析』は1つの目的変数に対して説明変数が1つだけ用いられる回帰分析のことです。
特に先ほど紹介した例のような「\(y=ax+b\)」の形の回帰式を求める方法を『線形単回帰分析』と言います。
先ほどの例では平均気温のみから売り上げを予測していました。
ここで、「平均気温」と「アイスクリーム1つあたりの金額」の2つの変数を用いて売り上げを予測すればより精度の高い予測ができると考えられます。
このように、1つの目的変数に対して複数の説明変数を用いて回帰分析を行う方法を『重回帰分析』と言います。
すなわち、重回帰分析は「\(y = a_1 x_1 + a_2 x_2 \dots + a_n x_n\)」というような形で表せます。
- 『単回帰分析』:1つの目的変数に対して1つの説明変数
- 『重回帰分析』:1つの目的変数に対して複数の説明変数
単回帰分析(最小二乗法)
単回帰分析は、1つの目的変数\(y\)に対して1つの説明変数\(x\)を用いて回帰式を求めます。
今回は「\(y=ax+b\)」の形で回帰式を求める線形単回帰分析について解説します。
以下のデータを用いて、なるべく精度の高い予測が可能な回帰式を求めることを考えます。

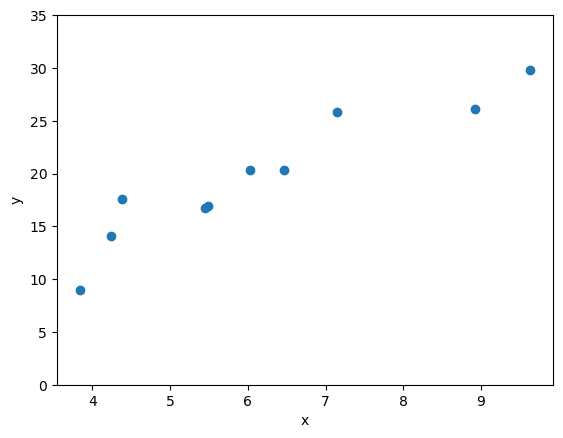
回帰式を求めるということはパラメーター\(a,b\)を求めることに等しいので、ちょうどよい(誤差が小さくなるような)\(a, b\)を求めることを目標にします。
これらのパラメーターを求める方法としてよく用いられるのが『最小二乗法』と呼ばれる方法です。
この方法では、回帰式と実際のデータの誤差の二乗和が最小となるようにパラメーターを求めます。
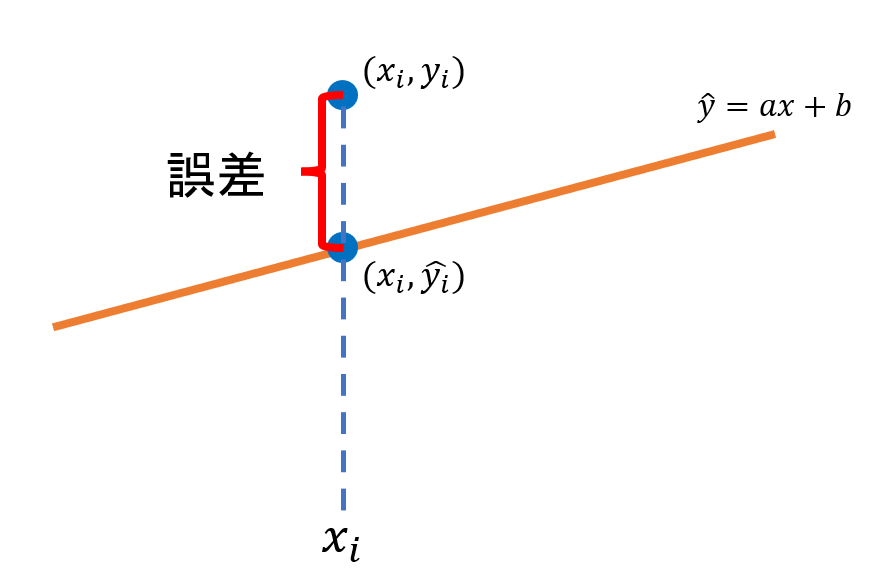
回帰式から予測される目的変数の値を\(\hat{y_i}\)、実際の目的変数の値を\(y_i\)とすると、誤差の二乗和\(S_e\)は以下の式で表されます。
$$
\begin{align*}
S_e &=\sum_{i=1}^{n} (y_i-\hat{y_i})\\
&=\sum_{i=1}^{n} (y_i-(ax_i+b))
\end{align*}
$$
\(x_i, y_i\)の値は既知ですので、これは\(a\)と\(b\)のみからなる2次式となります。
この値を最小化する\(a\)と\(b\)の値を求めるには、\(S_e\)を\(a\)と\(b\)それぞれで偏微分して0になるようにします。
すなわち、
$$ \frac{\partial S_e}{\partial a}=0 $$
$$ \frac{\partial S_e}{\partial b}=0 $$
を満たす\(a, b\)を求めます。
このようにして求めた\(a, b\)を「\(y=ax+b\)」の式に当てはめれば回帰式を求めることができます。
それでは、先ほど用意したデータ(\(x_i, y_i\))から\(a, b\)の値を求めてみましょう。

\(a, b\)の値を計算してみると、\(a=3.02\cdots, b=1.06\cdots\)という結果が得られました。
試しに「\(y=3.02x+1.06\)」のグラフをプロットに重ねて描いてみると以下のようになりました。
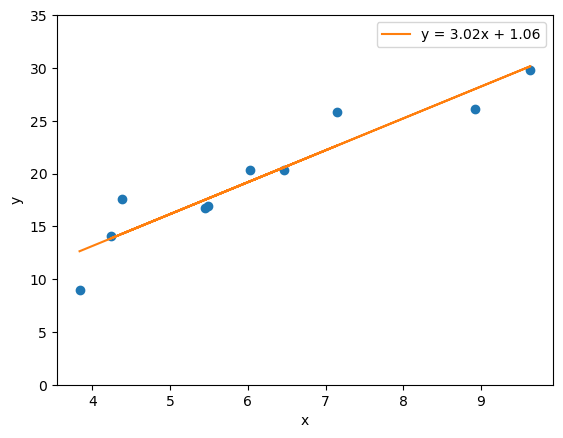
各点のちょうど真ん中あたりを通っていることが分かると思います。
重回帰分析
続いて『重回帰分析』の例を見てみましょう。
基本的な考え方は単回帰分析の場合と同様です。
今回は以下のデータを使用します。
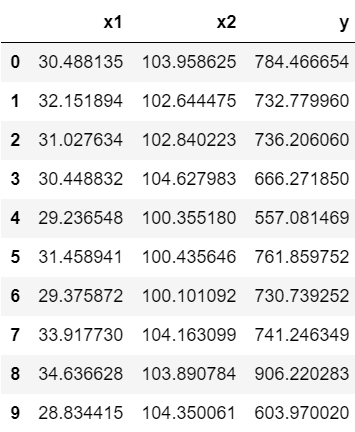
\(y\)を目的変数、\(x_1, x_2\)を説明変数として「\(y=a_1x_1+a_2x_2+b\)」という形の回帰式を求めていきます。
この場合の誤差の二乗和は以下の式で表されます。
$$ S_e=\sum_{i=1}^{n} (y_i-\hat{y_i})
\\ =\sum_{i=1}^{n} (y_i-(a_1x_{1, i}+a_2x_{2, i}+b))$$
(\(x_1, x_2\)の\(i\)番目の値をそれぞれx_1{1, i}, x_2{2, i}のように表記しています。)
この誤差の二乗和\(S_e\)を最小化するために、
$$ \frac{\partial S_e}{\partial a_1}=0 $$
$$ \frac{\partial S_e}{\partial a_2}=0 $$
$$ \frac{\partial S_e}{\partial a_b}=0 $$
を満たすパラメーター\(a_1, a_2, b\)の値をそれぞれ求めます。
今回は\(a_1=39.03\cdots, a_2 = -3.85\cdots, b=-98.66\cdots\)という結果が得られました。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
決定係数:回帰式を評価する
ここまで回帰式を求める方法を解説してきましたが、求めた式がどのくらい良いモデルであるかはグラフを見ただけでは判断できません。
そこで、以下の『決定係数』という指標によって回帰式を評価することを考えます。
$$ R^2=1-\frac{\sum_{i=1}^{n} (y_i-f(x_i))^2}{\sum_{i=1}^{n} (y_i-\bar{y})^2} $$
\(\bar{y}\)は目的変数\(y\)の平均値です。
決定係数の最大値は1で、値が1に近いほど良いモデルと言えます。
単回帰分析の例で求めた回帰式の決定係数を実際に求めてみると、\(R^2=0.88\cdots\)という結果が得られました。









