本連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第1章では、「基本統計量とは何か?」について扱います。
・分散は何を意味しているの?
・基本統計量にはどんなものがあるの?
このような疑問をお持ちの方はぜひご覧ください。
「基本統計量」について分かりやすく解説しています。
各基本統計量の「定義」と「意味」に注目して理解しましょう。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
基本統計量とは
基本統計量とは、データの特性を表すための指標のことです。
基本統計量の例として「平均」が挙げられます。
AクラスとBクラスの平均点を比較して、Aクラスの平均点の方が高ければ「Aクラスの方が頭がいい」と判断するでしょう。
このように基本統計量を用いることで、データを全て見なくても、ある程度データの特徴を捉えることができます。
基本統計量は「代表値」と「散布度」の2つに分けることができます。
- 代表値:データ全体の特徴を一つの数値で表す指標
- 散布度:データの散らばり具合を表す指標
では、具体的な「代表値」と「散布度」について解説していきます。
代表値
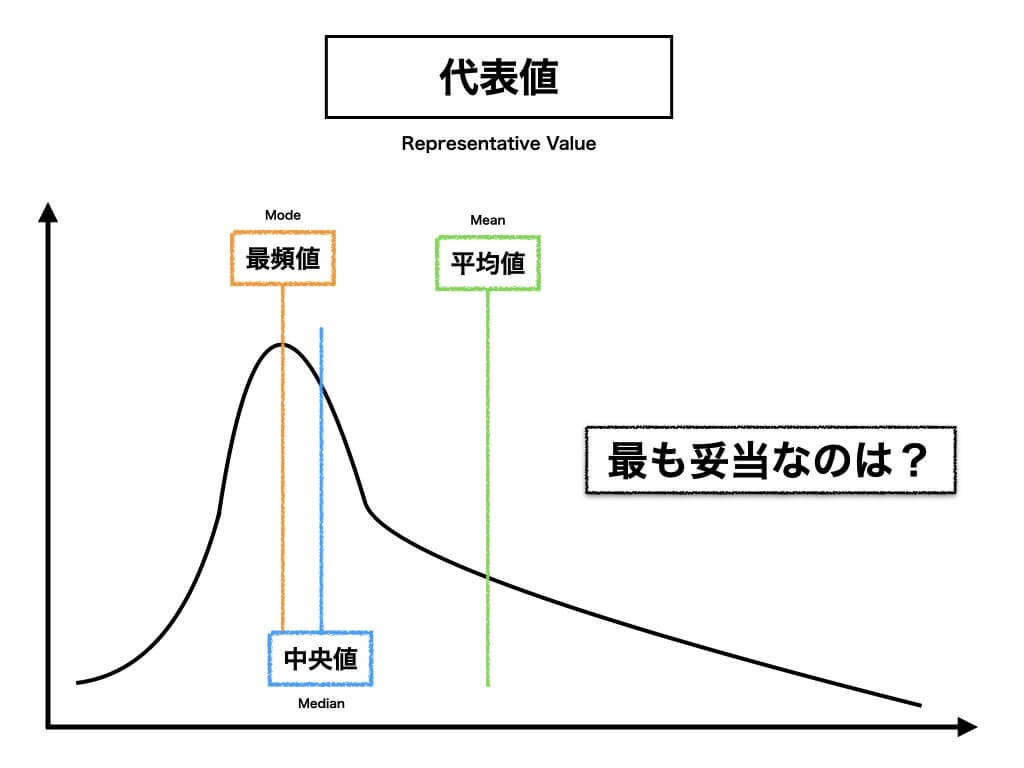 引用:https://evineko.com/stats/basics/mean-median/
引用:https://evineko.com/stats/basics/mean-median/
平均
まず初めに「平均」について説明していきます。
本記事では、一般的な「平均」を意味する「算術平均」以外にも、発展的な内容として「幾何平均」、「調和平均」も扱っています。
定義式とそれぞれの平均値を使う場面に注目しましょう。
算術平均
「算術平均」は、皆さんも馴染み深いであろう「一般的な平均」を指します。
「全てのデータの値を足し合わせた合計を、データの個数で割って算出される平均値」を算術平均と言います。
算術平均は、集団のデータの基準値を知りたいときによく用います。
以下に様々な種類の平均について紹介しますが、「平均」とだけを言われた場合は「算術平均」を指します。
n個のデータがあるとき、算術平均は以下のような式で定義されています。
$$ \bar{x} = \frac{x_1 + x_2 + \ldots + x_n}{n} $$
下記の練習問題で、具体例を確認しましょう
練習問題
以下の5人のテストの点数の平均を求めよ。
- Aさん:75点
- Bさん:85点
- Cさん:80点
- Dさん:100点
- Eさん;90点
\[
\begin{align*}
\bar{x} &= \frac{\scriptsize 75 + 85 + 80 + 100 + 90}{\scriptsize 5} \\
&= \frac{\scriptsize 430}{\scriptsize 5} \\
&= \scriptsize 86
\end{align*}
\]
幾何平均(発展)
幾何平均は「相乗平均」とも呼ばれ名前の通り、「データの値を掛け合わせた値のn乗根」を取ります。
n個のデータがあるとき、幾何平均は以下のような式で定義されています。
\[ x_G = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n} \]
「幾何平均」は「上昇率の平均」を求めるときに使用します。
具体的には
- 株価の平均上昇率
- 経済成長率
- 利益の伸び率
などで「幾何平均」が利用されています。
下記の練習問題で、具体例を確認しましょう。
練習問題
以下の大学生の貯金に関して、幾何平均(平均上昇率)を求めよ。
- 入学時の貯金が「¥100,000」
- 1年後の貯金が「¥200,000」
- 2年後の貯金が「¥600,000」
入学時→1年後の上昇率:2 (200%)
1年後→2年後の上昇率:3 (300%)
よって幾何平均は下記のように求められます。
\[
\begin{align*}
x_G &= \sqrt{\scriptsize 2 \times 3} \\
&= \sqrt{\scriptsize 6} \\
&\simeq {\scriptsize 2.45}
\end{align*}
\]
算術平均で上昇率を求めると、
$$ \frac{\scriptsize 2 + 3}{\scriptsize 2} = {\scriptsize 2.5} $$
この時、算術平均から貯金額を逆算すると
- 1年目の貯金額:100,000 × 2.5 = 250,000
- 2年目の貯金額:100,000 × 2.5 × 2.5 = 625,000
一方、幾何平均から貯金額を逆算すると
- 1年目の貯金額:100,000 × √6 ≒ 250,000
- 2年目の貯金額:100,000 × √6 × √6 = 600,000
上記より、この例では「算術平均」より「幾何平均」の方が貯金額を正しく評価できています。
調和平均(発展)
調和平均は、「各値の逆数の算術平均の逆数を取ったもの」です。
言葉では分かりにくいと思うので、下記の定義式を見て理解しましょう。
n個のデータがある時、調和平均Hは以下のように定義されます。
\[ \frac{\scriptsize 1}{H} = \frac{\scriptsize 1}{x_1} + \frac{\scriptsize 1}{x_2} + \ldots + \frac{\scriptsize 1}{x_n} \]
調和平均は、「比率の平均」を求める時に使用します。
具体的には、
- 平均時速
- 労働生産性
などで「調和平均」が用いられます。
下記の練習問題で、具体例を確認しましょう。
練習問題
60Kmの距離を、
- 行き:時速20Km/h
- 帰り:時速30Km/h
とする。
この時、往復での平均時速を調和平均で求めよ
定義式より調和平均は下記のように求められます。
\[
\begin{align*}
\frac{\scriptsize 1}{H} &= \frac{\scriptsize 1}{\scriptsize 20} + \frac{\scriptsize 1}{\scriptsize 30}\\
&= \frac{\scriptsize 50}{\scriptsize 600} \\
&\ = \scriptsize 12
\end{align*}
\]
中央値
中央値とは、数値を小さい方(大きい方)から順に並べた時に中央に位置する値です。
データ数が「偶数個」の場合は、教材によって定義が異なりますが、ここでは「中央の二つの値の平均」とします。
中央値はデータに歪みがあったり、外れ値があったりして、「平均値」を扱うのが不適切なときに使うことが多いです。
平均値が不適切な例は後述の「コラム」で扱うので、気になる方はご覧ください。
以下の例が、中央値を扱う活用例です。
- 年収(所得)を比較する
下記の練習問題で、具体例を確認しましょう。
練習問題
(1) [1, 2, 5, 8, 9]の中央値を求めよ。
(2)[2, 6, 4, 3, 9, 6, 11]の中央値を求めよ。
(1)の解答
[1, 2, 5, 8, 9]は小さい順に並んでいます。
中央は、3番目の「5」ですので、答えは「5」です。
(2)の解答
[2, 7, 4, 3, 6, 11]では、データを順に並べると
[2, 3, 4, 6, 7, 11]となります。
データは偶数個あり、中央の2つの値は「4」と「6」となので中央値は「5」となります。
最頻値(モード)
最頻値(モード)は、最も出現頻度の高い値のことを指します。
最頻値を調べることで、「そのデータの中で出やすい値が何か」を知ることができます。
具体的には
- 歪なサイコロを振って、どの目が出やすいか
などの場面で用います。
下記の練習問題で、具体例を確認しましょう。
練習問題
サイコロを振って以下の順でサイコロの目が出た。
この時、最頻値を調べよ。
[1, 4, 3, 5, 6, 4, 5, 3, 3, 2]
- 1の目が出た回数:1回
- 2の目が出た回数:1回
- 3の目が出た回数:3回
- 4の目が出た回数:2回
- 5の目が出た回数:2回
- 6の目が出た回数:1回
よって最頻値は「3」
最大値・最小値
最大値は、「データの中で最も大きい値」を指します。
最小値は「データの中で最も小さい値」を指します。
最大値・最小値を求めることで、データの範囲を知ることができます。
下記の練習問題で、具体例を確認しましょう。
練習問題
下記のリストはボール投げの記録を表している。
[23, 14, 8, 15 , 25, 12, 13, 21, 17]
最大値・最小値をそれぞれ求めよ。
リストを昇順に並べると
[8, 12, 13, 14, 15, 17, 21, 23, 25]
となります。
したがって
- 最小値:「8」
- 最大値:「25」
となります。
散布度
次に、データの散らばり具合を表す指標である「散布度」について解説していきます。
分散
分散は、「データの散らばり具合を表す値」です。
分散は、データの値と平均値の差の二乗の平均で求めることができます。
したがって、n個のデータがあるとき、分散は以下のような式で定義されています。
$$ s^2 = \frac{\scriptsize 1}{n} \sum_{i=1}^n (x_i – \bar{x})^2 $$
Σはiを1,2,3、…、nを代入したモノの和をとることを意味します。
すなわち、
$$ s^2 = \frac{\scriptsize 1}{n} \{(x_1 – \bar{x})^2 + (x_2 – \bar{x})^2 + \ldots + (x_n – \bar{x})^2\} $$
と表せます。
分散は
- 分散の値が大きい→データのばらつきが大きい
- 分散の値が小さい→データのばらつきが小さい
ということを意味します。
次に発展的内容として分散の式の意味について解説します。
分散は「平均からの散らばり具合を表す値」なので
$$ x_i – \bar{x} $$
すなわち、
「(データの値) – (平均値)」により、データの値が平均からどれだけ離れているかを計算します。
しかし、このまま和をとってしまうと
- 平均値:「5」
- 一番目のデータの値:「9」
- 二番目のデータの値:「1」
の時、
$$ (\scriptsize 9 – \scriptsize 5) + (- \scriptsize 1 – \scriptsize 5) = 0 $$
と1番目のデータと2番目のデータは平均から離れているのに合計すると、「0」となってしまいました。
このような事態を解決するために「二乗」することで、全て0以上の数として取り扱うことができ、平均値からの離れ具合を正しく評価できます。
$$ (\scriptsize 9 – \scriptsize 5)^2 + (\scriptsize 1 – \scriptsize 5)^2 = 32 $$
そして、和をとるだけでは、データ数がおおきくなるほど分散が大きくなる傾向があるので、最後にデータ数で割ります。
これによって分散の式が完成します。
下記の練習問題で、具体例を確認しましょう。
練習問題
(1)「分散」とは何を表す指標か?
(2) 以下の5人のテストの点数の分散を求めよ。
- Aさん:75点
- Bさん:85点
- Cさん:80点
- Dさん:100点
- Eさん;90点
(1) 分散は、「データの散らばり具合を表す値」
分散の「定義」と「意味」をしっかり覚えましょう。
(2)
\[
\begin{align*}
\bar{x} &= \frac{\scriptsize 75 + \scriptsize 85 + \scriptsize 80 + \scriptsize 100 + \scriptsize 90}{\scriptsize 5} \\
&= \scriptsize 86
\end{align*}
\]
よって分散は
\[
\begin{align*}
s^2 &= \frac{\scriptsize 1}{\scriptsize 5}\{(\scriptsize 75 – \scriptsize 86)^2 + (\scriptsize 85 – \scriptsize 86)^2 + (\scriptsize 80 – \scriptsize 86)^2 + (\scriptsize 100 – \scriptsize 86)^2 + (\scriptsize 90 – \scriptsize 86)^2\} \\
&= \scriptsize 74
\end{align*}
\]
標準偏差
標準偏差は、前述で説明した分散に対して平方根を取ると求めることができます。

平方根を取るだけなので、標準偏差も分散と同様、「データの散らばり具合を表す値」です。
すなわち、標準偏差は
- 標準偏差の値が大きい→データのばらつきが大きい
- 標準偏差が小さい→データのばらつきが小さい
ということを意味します。
「分散」とほぼ同じ意味なら、「標準偏差」って必要?
と疑問を持つ方もいるのではないでしょうか。
ここで、標準偏差を扱う理由について説明したいと思います。
分散は元のデータ(と平均の差)を2乗したものを使っているので、単位が元のデータの2乗となります。
そのため、標準偏差(分散の平方根を取ること)により、ばらつきの指標が本来のデータと同じ単位に揃えることができるため、標準偏差を導入しました。
下記の練習問題で、具体例を確認しましょう。
練習問題
以下の5人のテストの点数の分散を求めよ。
- Aさん:75点
- Bさん:85点
- Cさん:80点
- Dさん:100点
- Eさん;90点
分散は、前述の問題より
\[
\begin{align*}
s^2 &= \frac{\scriptsize 1}{\scriptsize 5}\{(\scriptsize 75 – \scriptsize 86)^2 + (\scriptsize 85 – \scriptsize 86)^2 + (\scriptsize 80 – \scriptsize 86)^2 + (\scriptsize 100 – \scriptsize 86)^2 + (\scriptsize 90 – \scriptsize 86)^2\} \\
&= \scriptsize 74 \\
\text{よって、標準偏差sは}\\
s &= \sqrt{\scriptsize 74} \approx \scriptsize 8.6
\end{align*}
\]
歪度・尖度
発展的な散布度として、「歪度(ワイド)」と「尖度(センド)」について紹介します。
歪度は、分布の非対称性を表す指標です。
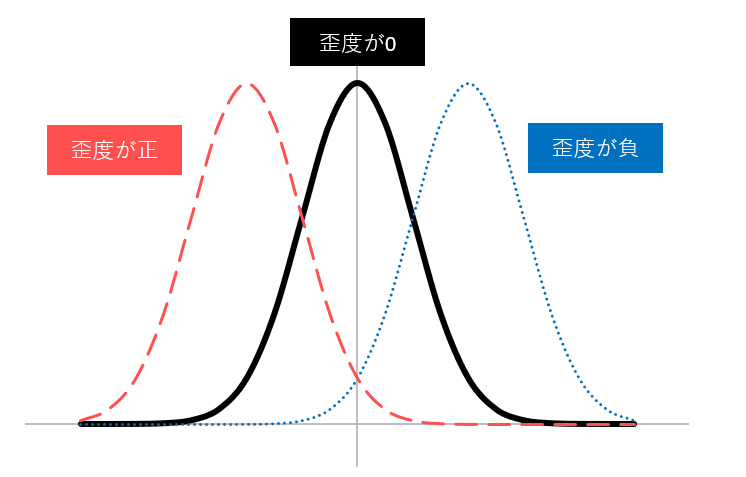
尖度は、分布の尖具合を表す指標です。
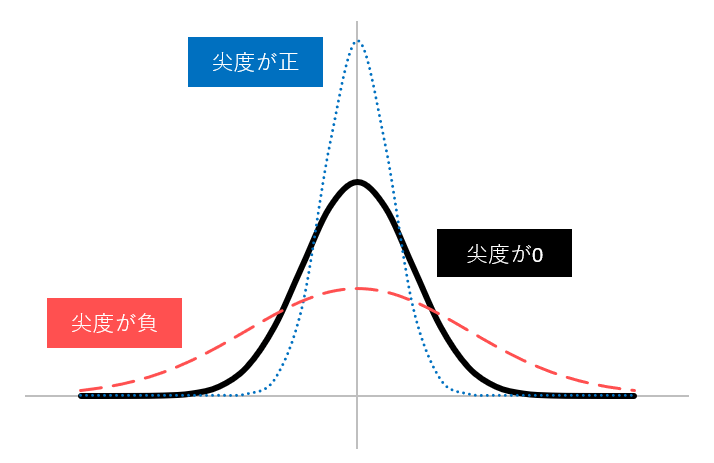
「歪度」、「尖度」の定義式については「期待値」が必要なので、式を理解するよりも上の画像のイメージを掴んでおきましょう。
期待値については、以下の記事で解説します。

期待値をすでに知っている方向けに、歪度と尖度の定義式を紹介します。
歪度
$$ \alpha_3 = \frac{[E(x-u)^3]}{\sigma^3} $$
尖度
$$ \beta_4 = \frac{[E(x-u)^4]}{\sigma^4} – 3 $$
なお、
- 「u」は「平均」
- 「σ」は「標準偏差」
を表しています。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
コラム
最後に今回扱った基本統計量について「平均値の問題点」と「偏差値とは」というコラムを掲載します。
実務や、普段の生活と関わりの深い内容なので興味がある方はぜひご覧ください。
平均値の問題点
偏差値とは
学校の試験や、模試の結果で「偏差値」を目安にしていた方も多いと思います。
今回学んだ基本統計量で、偏差値を理解したいと思います。
偏差値とは、テストを受けた集団の中で自分がどのくらいの位置にいるかを表す指標です。
そして「偏差値50」は平均的な点数を表します。
偏差値は以下のように定義されています。
$$ T = \scriptsize 10 \times \frac{x_i – \bar{x}}{s} + \scriptsize 50 $$
なお、$$ x_i:\text{自分の点数}\\ \bar{x}:\text{平均点}\\ s:\text{標準偏差} $$
を表します。
まず、(自分の点数) – (平均)により平均との差を求めています。
そして標準偏差で割ることで、
- ばらつきが多い場合は標準偏差が大きくなるため、偏差値が50から離れにくくなります。
- ばらつきが少ない場合は標準偏差が小さくなるため、偏差値が50から離れやすくなります。
「10を掛ける。50を足す。」という操作は、人間が理解しやすい数値に変換するためのものなので本質的には関係ありません。
偏差値の上限と下限って何?
と疑問を抱いている方もいると思います。
定義式より、理論上の偏差値は「マイナス無限大〜プラス無限大」まで取ることができます。(標準偏差が限りなく0に近い場合)
下記の練習問題で、偏差値を求めてみましょう。
練習問題
以下の2つの場合の偏差値を求めよ。
Aさんは、平均点60点、標準偏差10のテストで80点を取った。
Bさんは、平均点50点、標準偏差20のテストで80点を取った。
Aさんの偏差値
\[
\begin{align*}
T &= \scriptsize 10 \times \frac{\scriptsize 80 – \scriptsize 60}{\scriptsize 10} + \scriptsize 50 \\
&= \scriptsize 70
\end{align*}
\]
Bさんの偏差値
\[
\begin{align*}
T &= \scriptsize 10 \times \frac{\scriptsize 80 – \scriptsize 50}{\scriptsize 20} + \scriptsize 50 \\
&= \scriptsize 65
\end{align*}
\]
Bさんの方が、Aさんより平均に比べて良い点数をとっているにも関わらず、標準偏差の影響で偏差値はAさんの方が高いという結果が得られました。





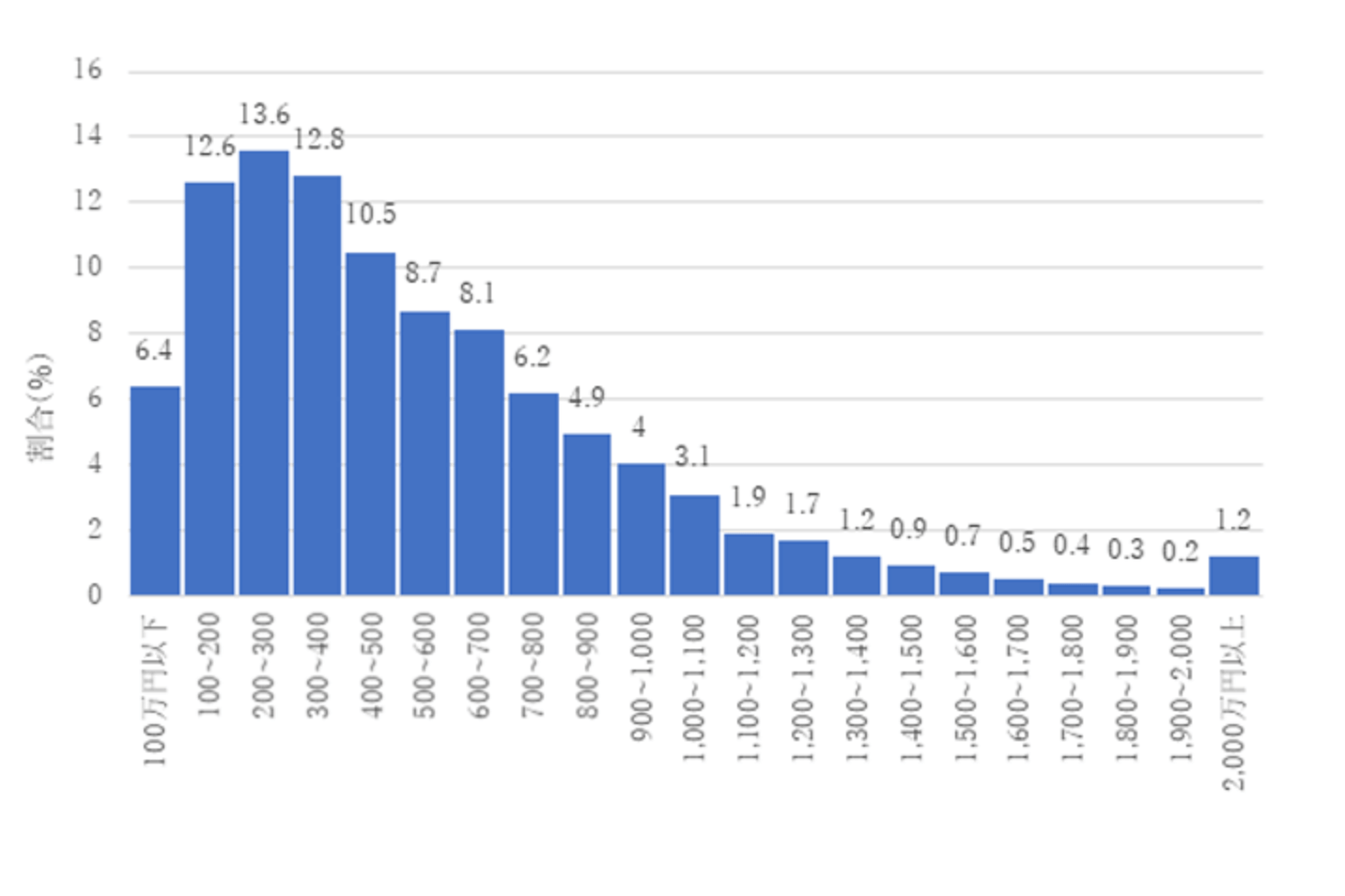 引用:https://heikinnenshu.jp/tokushu/householdincome.html
引用:https://heikinnenshu.jp/tokushu/householdincome.html




