連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第9章では、「大数の法則、中心極限定理」について解説します。
この記事では、大数の法則や中心極限定理の証明など高度な内容には焦点を当てず、それらのイメージやメリットを把握できるように解説しています。
中心極限定理は統計学を支える重要な定理なのでこの記事を読んでイメージを掴みましょう。
「母集団」や「標本」などの基本用語を確認したい方はこちらの記事をご確認ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
7章：母集団と標本
8章：標本平均・不偏分散
9章：中心極限定理
10章：母平均の推定(分散既知)
11章：母平均の推定(分散未知)
12章：仮説検定
13章：正規分布を用いた検定
14章：【t検定】母平均を検定
15章：【F検定】分散に差があるか？
16章：ウェルチの検定
17章：カイ2乗検定
18章：分散分析
19章：回帰分析
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
大数の法則
大数の法則のイメージを掴む
中心極限定理を紹介する前に、大数の法則(たいすうのほうそく)について解説します。
大数の法則はざっくり説明すると、試行回数を増やすほどデータの平均は真の平均(期待値)に近づくという法則です。
この法則は直感的にも理解しやすいと思います。
例として、サイコロの目をn回ふった時の平均値（期待値）について考えます。
サイコロは1から6までの目が均等に出現すると考えられるので、その母平均（期待値）は
$$ \frac{\scriptsize 1 + 2 + 3 + 4 + 5 + 6}{\scriptsize 6} = \scriptsize 3.5 $$
となります。
しかし、サイコロを1回振った場合、平均値は「3.5」にそれほど近くはならないでしょう。
一方、10回、100回、1000回と試行回数を増やしていくと、出た目の平均値が「3.5」に近づくイメージが持てるのではないでしょうか？
大数の法則は、「試行回数を増やすほどデータの平均は真の平均に近づく」という法則を数学的に表現したものです。
サイコロの目の平均値が「3.5」に近づく様子を、以下のグラフで確認しましょう。
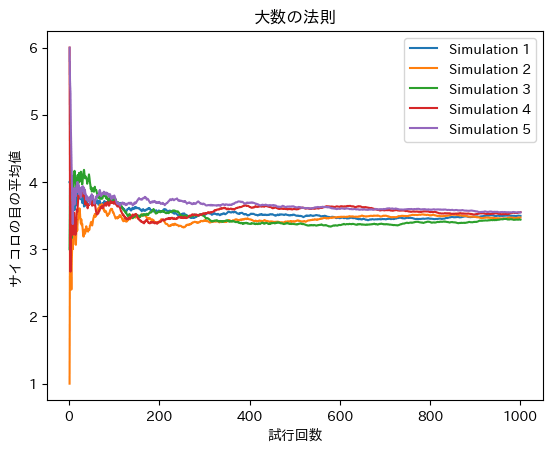
大数の法則の定義
発展的な内容として、大数の法則の数学的表記について解説します。
内容は上述のイメージと同じですが、少し表現が複雑になります。
興味のある方はぜひご覧ください。
大数の法則には、「大数の弱法則」と「大数の強法則」の2つの種類があります。
大数の弱法則
大数の弱法則は、標本\(X_1, X_2, \dots, X_n\)が独立同一分布に従い、平均μと分散\(\sigma^{\scriptsize2}\)が存在する時、任意の\(\epsilon > \scriptsize 0\)に対して、以下を満たす。
$$ \lim_{n \to \infty} P(|\frac{X_1 + X_2 + \dots + X_n}{n} – u| > \epsilon|) = 0 $$
大数の弱法則は、\(\bar{X}\)が\(u\)に確率収束することを意味します。
大数の強法則
大数の強法則は、標本\(X_1, X_2, \dots, X_n\)が独立同一分布に従い、平均μが存在する時、以下を満たす。
$$ P(\lim_{n \to \infty} \frac{X_1 + X_2 + \dots + X_n}{n} = u) = 1 $$
大数の強法則は、\(\bar{X}\)が\(u\)に概収束することを意味します。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
中心極限定理
中心極限定理とは
中心極限定理は、平均\(u\)、分散\(\sigma^{\scriptsize2}\)の母集団の分布が例外を除いてどんな分布であっても、標本の大きさnが十分大きいとき、標本平均\(\bar{X_n}\)の分布は近似的に平均\(u\)、分散\(\frac{\sigma^{\scriptsize2}}{n}\)の正規分布に従うことを意味しています。
正規分布を知らない方はぜひ下記の記事をご覧ください。
代表的な確率分布をまとめた記事となっています。
少し文章が長いのでポイントをまとめましょう。
- 母集団は平均\(u\)、分散\(\sigma^{\scriptsize2}\)であり、分布の形はなんでも良い
- 標本平均\(\bar{X_n}\)が、近似的に平均\(u\)、分散\(\frac{\sigma^{\scriptsize2}}{n}\)の正規分布に従う。
中心極限定理のメリット
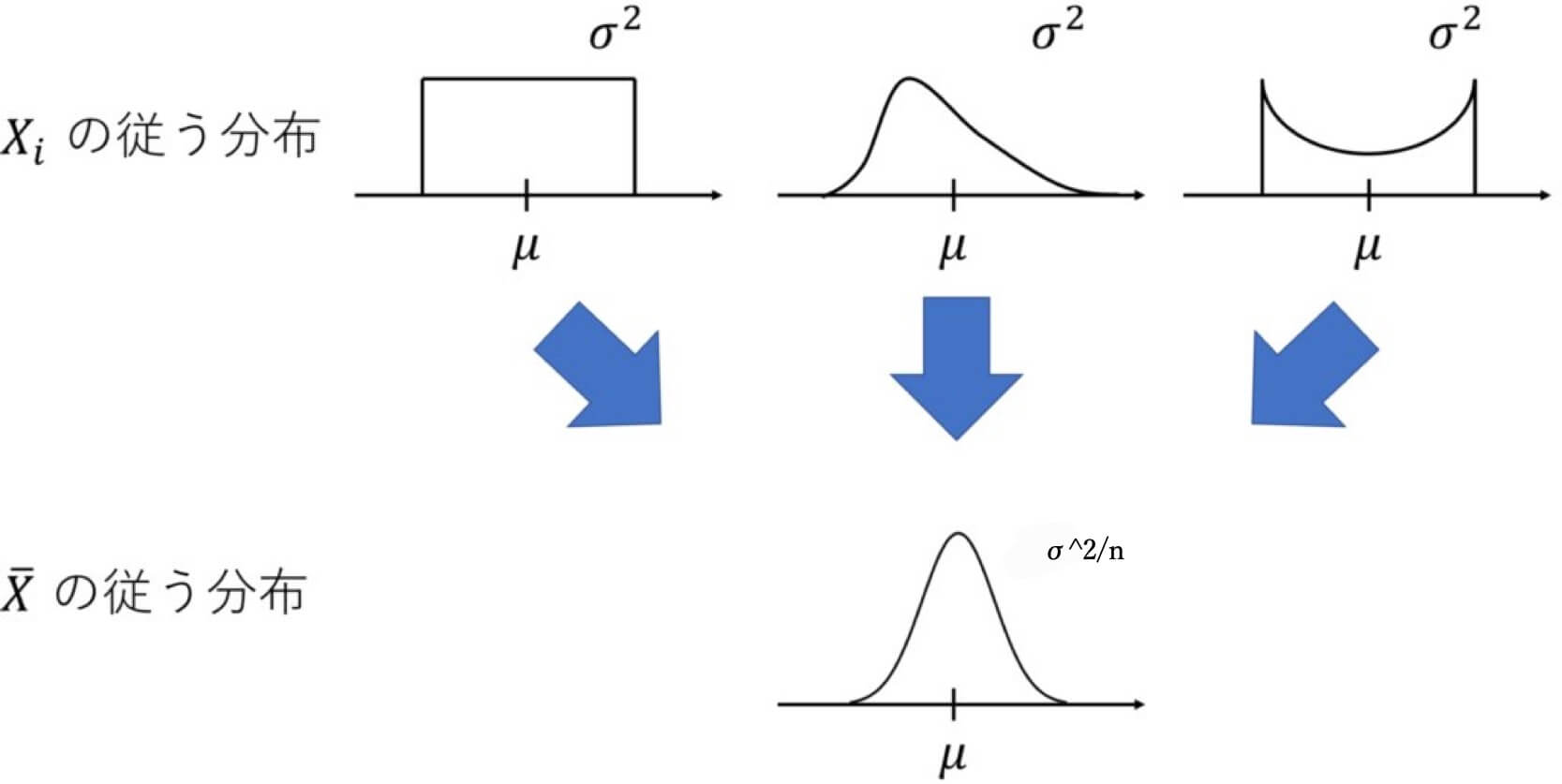
引用：https://daigakudenki.com/lln-clt/(修正あり)
中心極限定理を利用する最大の強みは、元々の確率変数がどのような分布であっても、その標本平均が正規分布に近似できる点です。
実際に、ある母集団を分析するときに「母集団の分布が複雑な分布に従っているため計算を進めることができない」や「そもそも母集団がどんな分布に従うか分からない」といった事態が多々あります。
一方、中心極限定理を使えば、標本平均が正規分布という簡単な分布により分析することが できます。
この中心極限定理は、次章以降で解説する区間推定や仮説検定などの統計的推論の基礎となっています。
正規分布が統計学で最も重要な分布と言われるのも、この中心極限定理が由来しています。
中心極限定理についてより理解するために補足説明をします。
どうして、分散が\(\frac{\scriptsize 1}{n}\)倍されるの？
と疑問に思った方もいるのではないでしょうか。
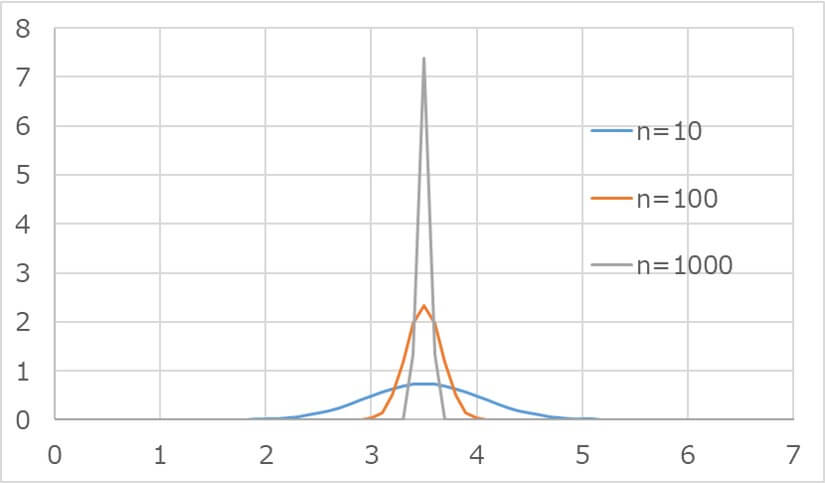
引用：https://qctoranomaki.com/sqc/statistics/central-limit/
分散が\(\frac{\scriptsize 1}{n}\)倍される理由は、データ数を大きくすればするほど、標本平均\(\bar{X_n}\)が真の平均\(u\)に近づいているためです。
例えば、データ数を母集団と同じ数や無限に近い数を集めた場合、大数の法則からも感覚的にも理解できるように「標本平均」と「真の平均」は一致します。
またデータ数を極端に大きくしなくてもデータ数を増やすと、標本平均は真の平均に近づくため、分散は徐々に小さくなり、グラフの概形はよりシャープになっていきます。
すなわち、中心極限定理は「標本平均」が「真の平均」に近づく揺らぎを表した定理ということもできます。
中心極限定理を使える条件
発展的な内容として、中心極限定理が成り立たない場合について解説していきます。
上記の中心極限定理の説明で、「例外を除いてどんな分布であっても標本の大きさnを十分大きいとき、標本平均\(\bar{X_n}\)の分布は近似的に正規分布に従う」と説明しました。
教材によっては「どんな場面でも中心極限定理は使用できる」と書いている場合もありますが、厳密には適用するための条件があるため本記事では「例外を除いて」と表現しています。
実際に中心極限定理を使う方は適用条件を確かめて使うようにしましょう。
中心極限定理を使える条件
- 独立な確率変数であること
- 同一の確率分布に従う確率変数であること
- 母平均の平均値と標準偏差（分散）が有限値であること
①、②はデータを集計するときに注意すれば問題ないのですが、③はデータの分布の「形」に関する内容なのでより一層の注意が必要です。
べき分布
平均や分散が発散する可能性のある分布として、べき分布があります。
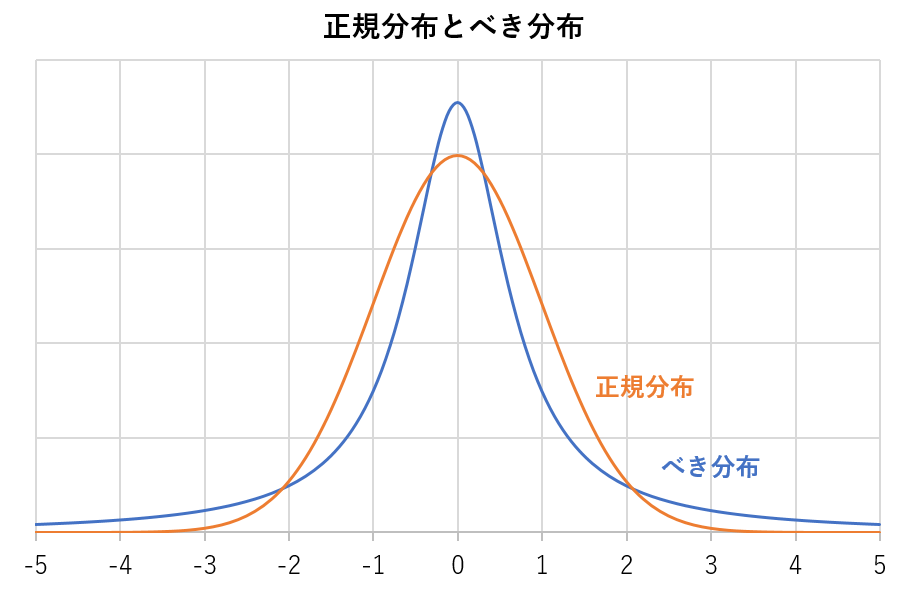
べき分布は、一部の要素が極端に大きな値を持ち、その他の要素は比較的小さい値を持つ特徴があります。
例えば、都市の人口分布、ウェブページのリンク数、地震のマグニチュード分布などがべき分布に従うことが知られています。
コーシー分布
平均値が不定であり分散が発散する分布として、コーシー分布があります。
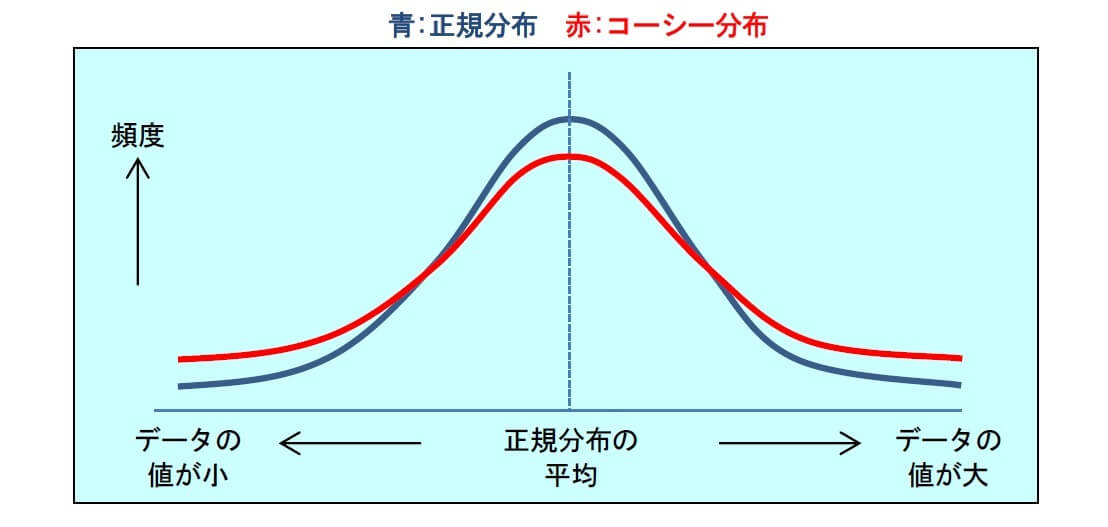
コーシー分布は、裾の部分で減衰が非常にゆっくりであるという特徴を持っています。
コーシー分布は、外れ値や極端な値をモデリングするのに使用されます。
また、物理学や金融学などの領域でもしばしば現れます。
特に、尖ったピークを持たずに極端な値を記述する必要がある場合に適した分布です。
興味がある方は、ぜひこれらの分布の式やさらに細かい特徴も調べてみてください。
