本連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第4章では、「条件付き確率・ベイズの定理」について解説します。
条件付き確率・ベイズの定理は機械学習にも関係してくる内容なので本記事を読んでマスターしましょう。
またコラムでは「モンティ・ホール問題」という直感で正しいと思える解答と、論理的に正しい解答が異なる問題を紹介します。
ぜひ最後までご覧ください。
確率のより基本的な内容から復習したい方は以下の記事をご覧ください。

本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
条件付き確率
条件付き確率の定義
Aを条件とするBの条件付き確率とは、事象Aが起こるという条件の元で事象Bが起こる確率ということを意味します。
Aを条件とするBの条件付き確率は『P(B|A)』と書き、式は以下のように定義されています。
$$
P(B|A) = \frac{P(A \cap B)}{P(A)}
$$
ベン図を用いてイメージで条件付き確率を理解しましょう。
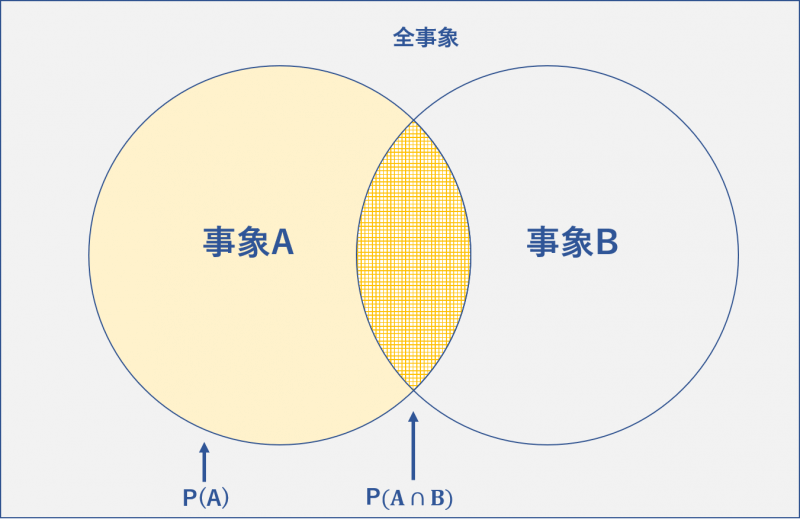
「事象Bが起こる確率」というのは、全事象(起こりうるすべての現象)に対して事象Bが起こる確率を表します。
一方、Aを条件とするBの条件付き確率は、事象Aを全事象とみなして、その世界で事象Bが起こる確率を表します。
具体例で確認しましょう。
例題
大小2つのサイコロがあります。
サイコロの目の和が偶数であるという条件の元で、サイコロの目の和が3の倍数である確率を求めましょう。
この場合、全事象は下図のように「36通り」あります。
そして、「2つの目のサイコロの和が偶数である」場合は以下の「18通り」となります。
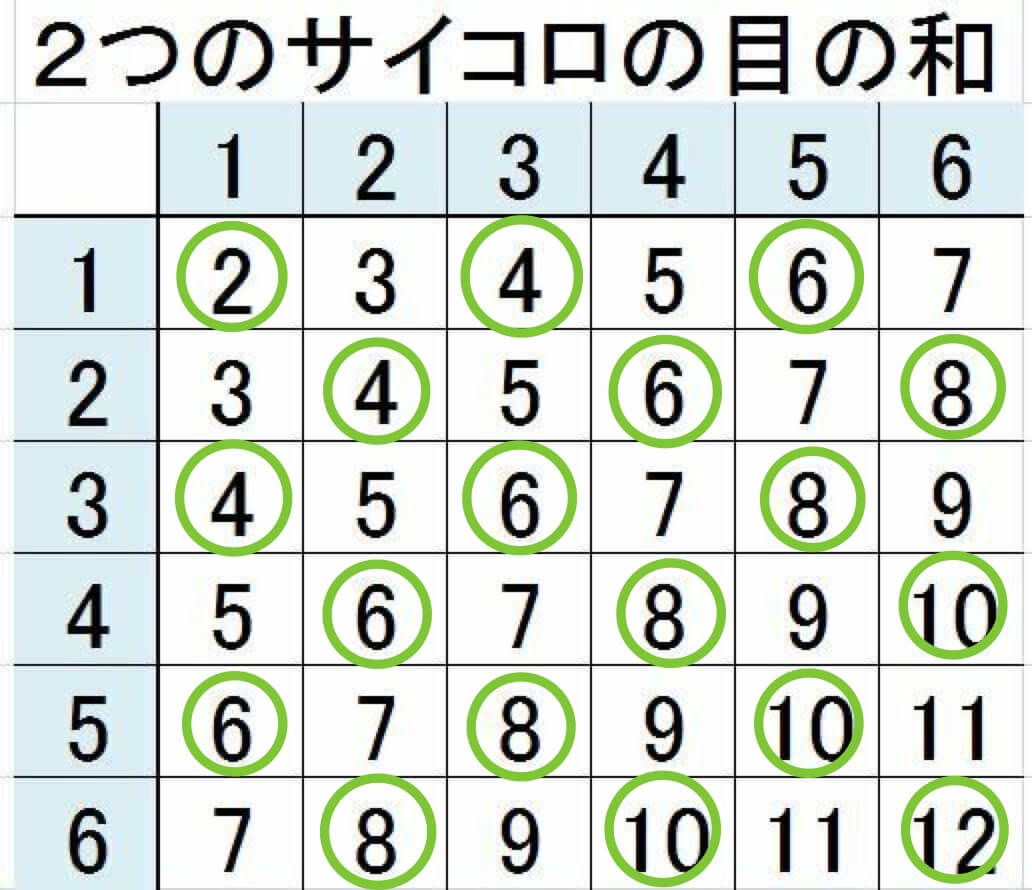
一方で「サイコロの目の和が3の倍数である確率」は「11通り」ですが、「サイコロの目の和が偶数であるという条件の元」では「5通り」となります。
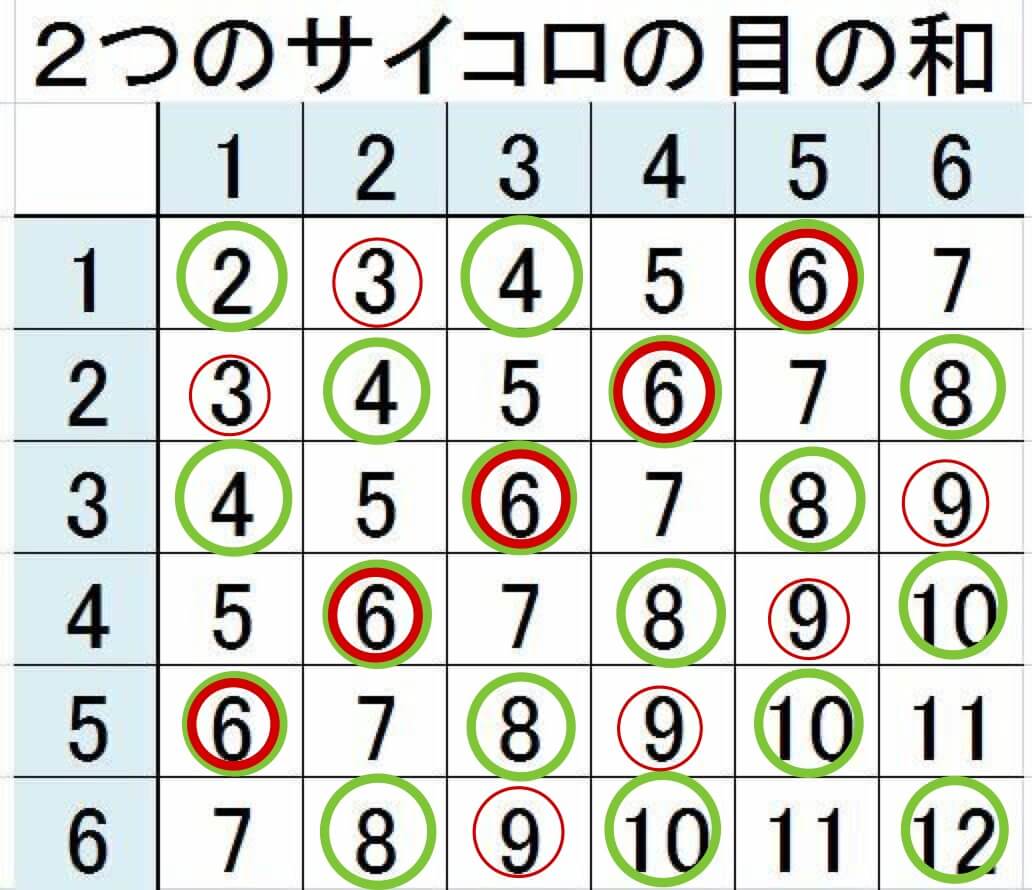
したがって、求める条件付き確率は
$$ \displaystyle\frac{5}{18}$$
となります。
独立
「事象Aと事象Bが独立である」とは、事象Aの起こる確率が事象Bに影響されない場合のことを言います。
「独立である」例として、
- コイントス
- サイコロを振る
があります。
1回目のコイントスやサイコロを振った結果が2回目のコイントスやサイコロを振った結果に影響を与えません。
「独立でない」例として、
- くじ引き(くじを戻さない)
があります。
当たりが3本、ハズレが7本のクジがあり、クジを二人で引く場合を考えます。
このとき前の人が当たりを引いたら、次の人はハズレを引きやすくなります。
一方、前の人がハズレを引いた場合、次の人は当たりを引きやすくなります。
このように独立でない場合、一つの事象が他の事象に影響を与えています。
そして独立である場合、以下の式が成り立ちます。
$$ P(A) = P(A|B) $$
$$ P(A \cup B) = P(A) \times P(B) $$
独立性を見分けることができれば、条件付き確率を楽に求めることができる場合があります。
条件付き確率:練習問題
練習問題1
袋の中に赤玉が3個、白玉が2個入っています。
袋からAさんが玉を引き、玉を元に戻さず、Bさんが玉を引きます。
このとき、Aさんが赤玉を引いた条件の元でBさんが赤玉を引いた確率を求めて下さい。
Aさんが赤玉を引く確率
$$ \frac{\scriptsize 3}{\scriptsize 5} $$
Aさんが赤玉を引いて、Bさんが赤玉を引く確率
$$ \frac{\scriptsize 3}{\scriptsize 5} \times \frac{\scriptsize 2}{\scriptsize 4} = \frac{\scriptsize 3}{\scriptsize 10} $$
以上より、Aさんが赤玉を引いた条件の元でBさんが赤玉を引いた確率
$$ \frac{\frac{\scriptsize 3}{\scriptsize 10}}{\frac{\scriptsize 3}{\scriptsize 5}} = \frac{\scriptsize 1}{\scriptsize 2} $$
練習問題2
袋の中に赤玉が3個、白玉が2個入っています。
袋からAさんが玉を引き、玉を元に戻して、Bさんが玉を引きます。
このとき、Aさんが赤玉を引いた条件の元でBさんが赤玉を引いた確率を求めて下さい
玉を元に戻す場合、「Aさんが玉を引く事象A」と「Bさんが玉を引く事象B」は独立なので
$$ P(A \cup B) = P(A) \times P(B) $$
が成り立ちます
よって、
$$ P(B|A) = \frac{P(A \cap B)}{P(A)} = P(B) $$
したがって、Bさんが赤玉を引く確率が、Aさんが赤玉を引いた条件の元でBさんが赤玉を引いた確率に等しいです。
Bさんが赤玉を引くのは
- Aさんが赤玉を引く → Bさんが赤玉を引く
- Aさんが白玉を引く → Bさんが赤玉を引く
の2パターンなので
$$ P(B|A) = P(B) = \frac{\scriptsize 3}{\scriptsize 5} \times \frac{\scriptsize 2}{\scriptsize 4} + \frac{\scriptsize 2}{\scriptsize 5} \times \frac{\scriptsize 3}{\scriptsize 4} = \frac{\scriptsize 3}{\scriptsize 5} $$
なお、練習問題1のように条件付き確率の定義通りに計算しても同様の結果が得られます。
ベイスの定理
ベイスの定理とは
ベイズの定理は、以下の式で表現されます。
$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} $$
ベイズの定理の証明
ベイズの定理は簡単に証明できるので興味がある方はぜひ、式を追ってみて下さい。
条件付き確率の定義式より、Bを条件とするAの条件付き確率は
\[
\begin{align*}
P(A|B) &= \frac{P(A \cap B)}{P(B)}\\
P(A \cap B) &= P(A|B) \times P(B)\\
\end{align*}
\]
同様にして、Aを条件とするBの条件付き確率は
\[
\begin{align*}
P(B|A) &= \frac{P(A \cap B)}{P(A)}\\
P(A \cap B) &= P(B|A) \times P(A)\\
\end{align*}
\]
したがって、
$$ P(A|B) \times P(B) = P(B|A) \times P(A) $$
上記の式を変形すると
$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} $$
が導けます。
ベイズの定理は一般的に下記のように書けます。
$$ P(A_i|B) = \frac{P(A_i) \cdot P(B|A_i)}{\sum_{j} P(A_j) \cdot P(B|A_j)} $$
ベイズの定理の意味・メリット
『Aを原因』、『Bを結果』である事象について考えます。
条件付き確率『P(B|A)』は、Aが起こった条件のもとでBが起こる確率を表していました。
一般的に条件付き確率は、原因(A)が起こった条件の元で結果(B)が起こる確率を考えます。
ベイズの定理では、「P(結果|原因)」を知っていれば、因果を逆転させたP(原因|結果)を求めることができるという点で有用となっています。
$$P(原因|結果) = \frac{P(結果|原因) \cdot P(A)}{P(B)} $$
「結果から原因を求める」ことよりも、「原因から結果を求める」方がはるかに簡単なことが多いです。
ベイズの定理を利用することで、因果関係を入れ替え、求めやすい確率から間接的に求めにくい確率を計算することができます。
ベイズの定理:練習問題
練習問題
全人口のうち、0.1%が病気Xにかかっているとします。
- 病気Xに罹患している人のうち、95%が正しく陽性と判定される
- 病気Xに罹患している人のうち、5% が誤って陰性と判定される
- 病気Xに罹患していない人にうち、20% が誤って陽性と判定される
- 病気Xに罹患していない人のうち、80%が正しく陰性と判定される
上記の条件で、陽性と判定された場合に病気にかかっている確率を求めましょう。
| 陽性 | 陰性 | |
| 病気Xに罹患している | 95% | 5% |
| 病気Xに罹患していない | 20% | 80% |
下記の条件より
- 病気Xにかかっている人のうち、95%が正しく陽性と判定される
- 病気Xにかかっている人のうち、5% が誤って陰性と判定される
- 病気Xにかかっていない人にうち、20% が誤って陽性と判定される
- 病気Xにかかっていない人のうち、80%が正しく陰性と判定される
$$ P(陽性|罹患) = \scriptsize 0.95 $$
$$ P(陰性|罹患) =\scriptsize 0.05 $$
$$ P(陽性|not 罹患) = \scriptsize 0.20 $$
$$ P(陰性|not 罹患) = \scriptsize 0.80 $$
全人口のうち、0.1%が病気Xにかかっているため
$$ P(罹患) = \scriptsize 0.001 $$
また、陽性と判定された人は
- 罹患している → 陽性
- 罹患していない → 陽性
の2パターンなので
$$ P(陽) = \scriptsize 0.001 \times \scriptsize 0.95 +\scriptsize 0.999 \times \scriptsize 0.20 \simeq \scriptsize 0.20$$
陽性と判定された場合に病気にかかっている確率は『P(罹患|陽性)』なので
ベイズの定理より、
\[
\begin{align*}
P(\text{罹患}|\text{陽性}) &= \frac{P(\text{陽性}|\text{罹患}) \cdot P(\text{罹患})}{P(\text{陽性})} \\
&= \frac{\scriptsize 0.95 \cdot \scriptsize 0.001}{\scriptsize 0.20} \\
&= \scriptsize 0.00475
\end{align*}
\]
よって、陽性と判定されて病気にかかっている確率は「0.475%」となります。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
コラム:モンティ・ホール問題
モンティ・ホール問題は、「直感で正しいと思える解答と、論理的に正しい解答が異なる問題」として有名です。
モンティ・ホール問題は、モンティ・ホールアメリカが司会を務めるテレビ番組「Let’s Make a Deal」が取り上げたことが名前の由来となっています。
では、実際に問題を見ていきましょう。

モンティ・ホール問題
- 3つのドアの先に「1つに賞品」が、「残りの2つにヤギ(ハズレ)」がランダムに入っていて、挑戦者が賞品のドアを選べば、その商品をもらえる
- 挑戦者はまずドアを1つ選ぶ
- 出題者(モンティさん)が残りのドアのうち、ヤギの入っているドアを1つ開ける
- あなたはドアを選びなおしてよいと言われる
確率的に、挑戦者はドアを選び直すべきでしょうか?
直感的に
ドアを変えても、変えなくても賞品を当てる確率は変わらなそう
と考える方も多いのではないでしょうか。
しかし、実際は「選ぶドアを変えた方が得」です。
モンティ・ホール問題を簡単に解説していきます。
ドアをそれぞれ「当たりのドア」、「ハズレのドア(1)」、「ハズレのドア(2)」とします。
そして、挑戦者が初めにドアを1つ選ぶ時、それぞれのドアを選ぶ確率は「1/3」です。
あらかじめ、ドアを変えるか・変えないか選択しておくと分かりやすくなります
ドアを変えない選択をしていた場合
当たりのドア、ハズレのドア(1)、ハズレのドア(2)のうちから「当たりのドア」を引く確率は「1/3」です。
ドアを変えないため、当たりのドアを引いた確率は「1/3」
ドアを変える選択をしておいた場合
初めにドアを選び、出題者がハズレのドアを一つ開け、選ぶドアを変えた場合、以下の3つのパターンがあります。
- 当たりのドア → ハズレのドア
- ハズレのドア(1) → 当たりのドア
- ハズレのドア(2) → 当たりのドア
ドアを変えた場合、当たる確率は「2/3」となります。
この問題のポイントは「最初に挑戦者がハズレを選ぶ確率の方が高く(2/3)、かつモンティが「確実に」ハズレの扉を開いてくれる点」です。
初めて聞く人にとっては直感的ではない結果を持っているため、確率論や統計学の面白い例とされています。
引用:https://digimarl.com/syllabus/data-science-no4/
引用:https://otonano-shumatsu.com/images/328889/1