連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第5章では、「期待値」について解説します。
期待値は、数学の中でも日常生活に役立つ考え方です。
期待値を知っておくと、人生の中で得をする判断を下せる場面が増えます。
期待値の意味から、定義・性質を丁寧に解説しています。
また、コラムとして「プロスペクト理論」という期待値と心理学をミックスした理論を紹介します。
「プロスペクト理論」は、マーケティングや人材育成にも関わってくるので、ぜひ最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
7章：母集団と標本
8章：標本平均・不偏分散
9章：中心極限定理
10章：母平均の推定(分散既知)
11章：母平均の推定(分散未知)
12章：仮説検定
13章：正規分布を用いた検定
14章：【t検定】母平均を検定
15章：【F検定】分散に差があるか？
16章：ウェルチの検定
17章：カイ2乗検定
18章：分散分析
19章：回帰分析
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
期待値とは
期待値のイメージ
期待値の定義式を解説するために、「期待値が何を意味しているか」を簡単に解説します。
ここで期待値のイメージを理解しましょう。
期待値とは「１回の試行で、どれくらいの値が出ると期待できるか」を表しています。
具体例で確認しましょう。
具体例1
1%の確率で、1000円得られるくじ引きがあるとします。
このくじの期待値はいくらでしょうか？
1%の確率で1000円得られるため、このくじは「100回引いて1回、1000円得られる」と解釈できます。
そのため、1回の試行で期待できる値は
$$ 0.01 \times 1000 = 10円 $$
となります。
これで期待値が計算できました。
すなわち、期待値は「1回引くと10円得ると期待できる」と解釈できます。
実生活では、店側が「20円」や「100円」などの参加費を設定することで利益を出すでしょう。
期待値のイメージは理解できたでしょうか？
次に期待値の定義式について紹介します。
期待値の定義
確率変数Xの期待値「E(X)」は下記の定義式で計算できます。
$$ E(X) = \sum_x x \cdot f(x) $$
Σを使わないと下記のように表現できます。
$$ E(X) = x_1f(x_1) + x_2f(x_2) + \ldots $$
なお、
- x：確率変数Xがとる値
- f(x)：「x」となる確率
を表します。
変数Xがあって、それぞれの値をとる確率が決まっているときXを確率変数と言います。
例えば、サイコロの確率変数Xは「1から6までの整数の値を取る変数」となります。
具体例で期待値の定義を理解しましょう。
具体例
サイコロの出る目の期待値を求めましょう
サイコロの出る目の確率はそれぞれ「1/6」です。
先ほど学んだ確率変数を
$$ X = 1 \text{で}、 f(x) = \frac{\scriptsize 1}{\scriptsize 6} $$
$$ X = 2 \text{で}、 f(x) = \frac{\scriptsize 1}{\scriptsize 6} $$
$$ \text{etc} $$
と表します。
よって、期待値E(X)は
$$ E(X) = \frac{\scriptsize 1}{\scriptsize 6} \times \scriptsize 1 + \frac{\scriptsize 1}{6} \times \scriptsize 2 + \ldots + \frac{\scriptsize 1}{\scriptsize 6} \times \scriptsize 6 = \scriptsize 3.5 $$
となります。
上記で定義した期待値は、確率変数Xが離散型(飛び飛びの値)の場合に利用できます。
例えば、サイコロの目は、「1」、「2」、…というように飛び飛びの値を取ります。
一方、確率変数Xが連続型の場合、期待値は下記の式で定義されています。
$$ E(X) = \int_{- \infty}^{\infty} x \cdot f(x)dx $$
Σを「積分」に置き換えただけで本質的な意味は変わりません。
期待値と平均値の違い
期待値と平均値はとても深い関わりがあるので、平均値と比較することでより「期待値」を深く理解しましょう。
平均について詳しく知りたい方は下記の記事をご覧ください。
平均値と期待値の違いは、期待値はこれから行う試行に対して予測される平均値で、既に試行した結果に対しては平均値といいます。
具体例で確認しましょう。
上記の例題でサイコロの目の期待値は「3.5」と求めることができました。
期待値は、「サイコロを振る前に、サイコロの出る目の平均値を考える」ことと同じ意味です。
このように考えると
$$
\begin{align*}
& \frac{\scriptsize 1 + 2 + 3 + 4 + 5 + 6}{\scriptsize 6} \\
&= \frac{\scriptsize 1}{\scriptsize 6} \times \scriptsize 1 + \frac{\scriptsize 1}{6} \times \scriptsize 2 + \ldots + \frac{\scriptsize 1}{\scriptsize 6} \times \scriptsize 6
\end{align*}
$$
と期待値と同様の式を得ることができました。
一方、平均値は過去にサイコロを振って「1」、「5」、「6」の目が出た場合に
$$ \frac{\scriptsize 1+5+6}{\scriptsize 3} = \scriptsize 4 $$
といった風に「得られた結果」から算出します。
サイコロが歪で1が出にくく、6が出やすい場合を考えます。
例として
- 「１」の出る確率：「1/12」
- 「６」の出る確率：「1/4」
- 他の目が出る確率：「1/6」
とします。
このとき、予想される平均値(期待値)は例えば下記ように上がるでしょう。
$$
\frac{\scriptsize 1}{\scriptsize 12} \times \scriptsize 1 + \frac{\scriptsize 1}{6} \times \scriptsize 2 + \ldots + \frac{\scriptsize 1}{\scriptsize 4} \times \scriptsize 6
$$
すなわち、期待値とは「確率によって重み付けした平均値」と言えます。
また、言い換えると試行を重ねると「平均」が「期待値」に収束するとも言えます。
練習問題
練習問題1
「表が出る確率が0.6」、「裏が出る確率が0.4」の歪なコインがあるとします。
このコインを１回投げ、表が出た場合は2ポイント、裏が出た場合は1ポイント得られるとします。
コインを1回投げたときの期待値はいくつでしょうか？
確率変数Xを
- 表が出る場合：X = 1
- 裏が出る場合：X = 2
と定義します。
したがって、問題文より
$$ f(X = {\scriptsize 1}) = \frac{\scriptsize 3}{\scriptsize 5}\quad (\text{表が出る確率})$$
$$ f(X = {\scriptsize 0}) = \frac{\scriptsize 2}{\scriptsize 5}\quad (\text{裏が出る確率})$$
と書けます。
表が出た場合は2ポイント、裏が出た場合は1ポイント得られるので、期待値E(X)は
$$ E(X) = \scriptsize 2 \times \frac{\scriptsize 3}{\scriptsize 5} + 1 \times \frac{\scriptsize 2}{\scriptsize 5} = \scriptsize 1.6 $$
練習問題2(発展問題)
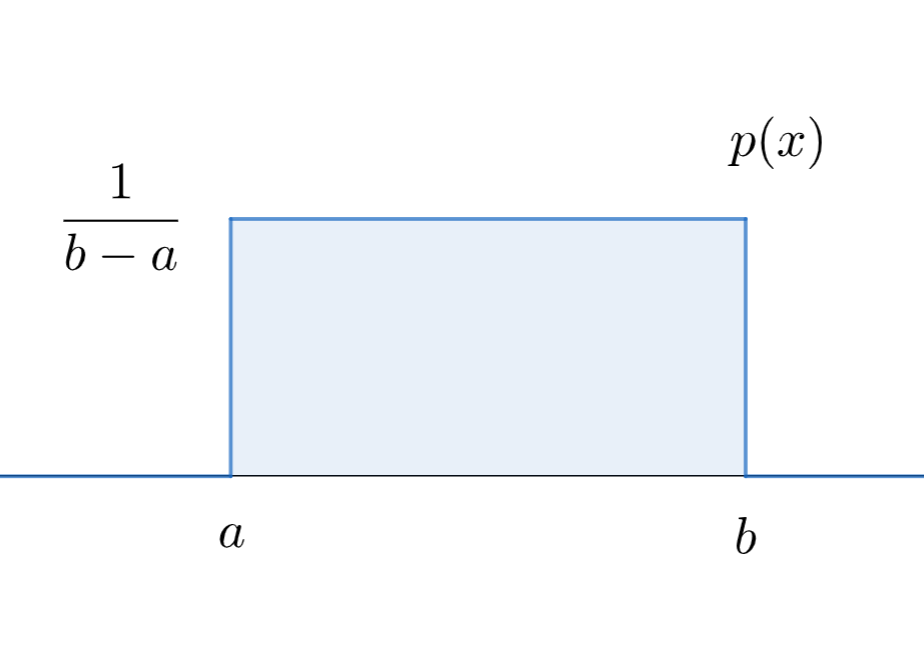
次のような連続一様分布を考えます。
$$
\begin{align*}
f(x) &= \frac{\scriptsize 1}{b – a} \quad (a \leq x \leq b) \\
f(x) &= 0 \quad (x < a, \, x > b)
\end{align*}
$$
この連続一様分布の期待値を求めましょう。
引用：https://mathlandscape.com/unif-distrib/
期待値の定義式より、
$$
\begin{align*}
E(X) &= \int_{- \infty}^{\infty} x \cdot f(x)dx \\
&= \int_{a}^{b} x \cdot \frac{\scriptsize 1}{b – a}dx \\
&= \frac{b^{\scriptsize 2} – a^{\scriptsize2}}{{\scriptsize 2}(b – a)}\\
&= \frac{a + b}{\scriptsize 2}\\
\end{align*}
$$
期待値の性質
期待値は、4つの重要な性質を満たします。
下記の性質を知っておくことで、期待値を簡単に求めることができる場合があるのでぜひマスターしましょう。
簡単に証明もできるので、興味がある方はぜひご覧ください。
なお、証明は離散型の場合に限定して記載しますが連続型でも同様の方法で証明することができます。
性質1 ：定数の期待値
期待値の一つ目の性質は、定数の期待値は定数になります。
$$ E(c) = c $$
cは定数を表します。
証明
起こりうるすべての確率の和が「1」であることに注意すると
$$
\begin{align*}
E(c) &= \sum_x c \cdot f(x) \\
&= c \sum_x f(x) \\
&= c \cdot 1 \quad (\sum_x f(x) = 1)
\end{align*}
$$
性質2：確率変数の定数倍
期待値の2つ目の性質は、「確率変数Xを定数倍した期待値は、確率変数Xの期待値の定数倍に等しい」です。
$$ E(cX) = c\times E(X) $$
Xは確率変数、cは定数を表します。
証明
$$
\begin{align*}
E(cX) &= \sum_x cx \cdot f(x) \\
&= c \sum_x x \cdot f(x)\\
&= c \times E(X)\\
\end{align*}
$$
性質3：確率変数と定数の和
期待値の3つ目の性質は、「確率変数Xに定数cを足した期待値は、確率変数Xの期待値とcの和に等しい」です。
$$ E(X+c) = E(X) + c $$
Xは確率変数、cは定数を表します。
証明
$$
\begin{align*}
E(X+c) &= \sum_x (x+c) \cdot f(x) \\
&= \sum_x x \cdot f(x) + \sum_x c \cdot f(x) \\
&= E(X) + E(c)\\
&= E(X) + c
\end{align*}
$$
性質4：確率変数と確率変数の和
期待値の4つ目の性質は、「確率変数Xに確率変数Yを足した期待値は、確率変数Xの期待値と確率変数Yの期待値の和に等しい」です。
$$ E(X+Y) = E(X) + E(Y) $$
Xは確率変数、Yも確率変数を表します。
この性質の証明は少し高度であるため割愛しますが、式は覚えやすく便利なので使えるようにしましょう、
練習問題
練習問題
確率変数Xの平均をuとすると、分散V(X)は
$$ V(X) = E\{(X – u)^{\scriptsize 2}\} $$
と定義できます。
uは平均(定数)である。
以下の分散の公式が成り立つことを証明してください。
$$ V(X) = E(X^{\scriptsize 2}) – u^{\scriptsize 2} $$
なお
$$ E(X) = u $$
に注意しましょう。
分散について詳しく知りたい方は下記の記事をご覧ください。
上記の性質より、
$$
\begin{align*}
V(X) &= E\{(X – u)^{\scriptsize 2}\} \\
&= E(X^{\scriptsize 2} – 2uX + u^{\scriptsize 2}) \\
&= E(X^{\scriptsize 2}) + E(-{\scriptsize2}uX) + E(u^{\scriptsize 2})\quad (\text{性質3,4})\\
&= E(X^{\scriptsize 2}) – {\scriptsize 2}uE(X) + u^{\scriptsize 2}\quad (\text{性質1,2})\\
&= E(X^{\scriptsize 2}) – u^ {\scriptsize 2}\quad (E(X) = u)
\end{align*}
$$
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
コラム：プロスペクト理論
プロスペクト理論とは
従来の経済学では、「人間は常に合理的な行動をする」とされてきました。
しかし、心理学と経済学を組み合わせた学問である行動経済学では、「人は直感や感情によって合理的ではない判断をする」ことを前提にその理由や理論を研究しています。
そして、この行動経済学はビジネス、マーケティングに広く応用されています。
プロスペクト理論は、心理学者のダニエル・カーネマンとエイモス・トベルスキーによって提唱され、この行動経済学の基礎を築きました。
プロスペクト理論の内容の紹介に入る前に、以下の質問について考えてみてください。
質問1
以下の2つの選択肢①と②のうち、あなたはどちらを選択しますか？
①：100%の確率で、100万円もらえる
②：50%の確率で200万円を貰えるが、10%の確率で1円も貰えない。
質問2
以下の2つの選択肢AとBのうち、あなたはどちらを選択しますか？
A：100%の確率で、100万円を失う
B：50%の確率で200万円を失うが、10%の確率で1円も失わない。
今回学んだ期待値を計算すると、
| ①の場合 | + 100万円 |
|---|---|
| ②の場合 | + 100万円 |
| Aの場合 | – 100万円 |
| Bの場合 | – 100万円 |
となります。
したがって、計算上では、どちらの答えを選んでもおかしくありません。
しかし一般的には、質問1の場合は「①」、質問2の場合は「B」と答える方が多いようです。
プロスペクト理論では、「人間は目の前に利益があると、利益が手に入らないというリスクの回避を優先し、損失を目の前にすると、損失そのものを回避しようとする傾向」があるということを述べています。
さらに簡単に言うと、人間は「利益を得る選択」よりも「損失を避ける選択」を好んでする傾向にあるということです。
選択肢が下記のように変わった場合、期待値に沿った選択ができるでしょうか？
- ②：50%の確率で210万円を貰えるが、50%の確率で1円も貰えない。
- B：50%の確率で210万円を失うが、50%の確率で1円も失わない。
プロスペクト理論は、私たちの日常生活でも広く活用されており、知らず知らずのうち自分が損をする決断を下していることがあるかもしれません。
期待値を考えることは、自分にとって有益な意思決定をする手助けとなるでしょう。
日常生活で使われているプロスペクト理論
プロスペクト理論は、普段の日常生活やマーケティングにも表れている内容なので具体例を確認していきましょう。
期間限定キャンペーン
「期間限定に弱い！」「期間限定だといわれるものには全て手を出しておきたい！」という方もいらっしゃるのではないでしょうか。
期間限定キャンペーンは、プロスペクト理論を応用した優れたマーケティング手法の一つです。
企業が製品の通常価格よりも期間限定で割引を提供する場合、「その期間に商品を購入しないと普段より損してしまう」という損失回避の心理が働きます。
この心理は、我々の購買意欲をかき立て、限られた期間内に購入を促進します。
株・Fx
株やFXの投資において、
・株価が上昇しているにもかかわらず、早めに売却する
・損失が出ていてもなかなか手を引くことができない
といったことがあります。
これらの行動も、投資家がプロスペクト理論に基づく「損失回避」の心理に影響を受けている代表的な例です。
市場参加者が理性的な判断を下す際には、これらの心理的な要因に注意を払うことが重要です。
